题目内容
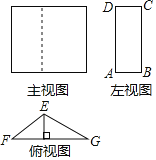
【题目】某几何体的三视图如图所示,已知在△EFG中,FG=18cm,EG=12cm,∠EGF=30°;在矩形ABCD中,AD=16cm.
(1)请根据三视图说明这个几何体的形状.
(2)请你求出AB的长;
(3)求出该几何体的体积.
【答案】(1)三棱柱;(2)6cm;(3)864cm3.
【解析】
(1)根据三视图,可知这个几何体上下两个底面都是三角形的,侧面是长方形的,因此这个几何体是三棱柱;
(2)AB的长就是俯视图中三角形FG边上的高,
(3)求出俯视图中FG上的高,进而求出三棱柱底面面积,AD=16,进而求出体积.
(1)三棱柱;
(2)AB=sin30°×EG=![]() ×12=6cm,
×12=6cm,
(3)V=SH=![]() ×18×6×16=864cm3,
×18×6×16=864cm3,
答:该几何体的体积为864cm3,

练习册系列答案
相关题目