题目内容
【题目】某公司研发了一款成本为50元的新型玩具,投放市场进行试销售.其销售单价不低于成本,按照物价部门规定,销售利润率不高于90%,市场调研发现,在一段时间内,每天销售数量y(个)与销售单价x(元)符合一次函数关系,如图所示:
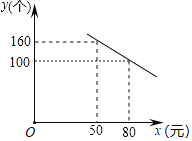
(1)根据图象,直接写出y与x的函数关系式;
(2)该公司要想每天获得3000元的销售利润,销售单价应定为多少元
(3)销售单价为多少元时,每天获得的利润最大,最大利润是多少元?
【答案】(1)y=﹣2x+260;(2)销售单价为80元;(3)销售单价为90元时,每天获得的利润最大,最大利润是3200元.
【解析】
(1)由待定系数法可得函数的解析式;
(2)根据利润等于每件的利润乘以销售量,列方程可解;
(3)设每天获得的利润为w元,由题意得二次函数,写成顶点式,可求得答案.
(1)设y=kx+b(k≠0,b为常数)
将点(50,160),(80,100)代入得
![]()
解得![]()
∴y与x的函数关系式为:y=﹣2x+260
(2)由题意得:(x﹣50)(﹣2x+260)=3000
化简得:x2﹣180x+8000=0
解得:x1=80,x2=100
∵x≤50×(1+90%)=95
∴x2=100>95(不符合题意,舍去)
答:销售单价为80元.
(3)设每天获得的利润为w元,由题意得
w=(x﹣50)(﹣2x+260)
=﹣2x2+360x﹣13000
=﹣2(x﹣90)2+3200
∵a=﹣2<0,抛物线开口向下
∴w有最大值,当x=90时, w最大值=3200
答:销售单价为90元时,每天获得的利润最大,最大利润是3200元.

【题目】已知:二次函数![]()
![]() 中的
中的![]() 和
和![]() 满足下表:
满足下表:
| … |
| 0 | 1 | 2 | 3 | … |
| … | 3 | 0 |
| 0 | m | … |
(1) 观察上表可求得![]() 的值为________;
的值为________;
(2) 试求出这个二次函数的解析式;
(3) 若点A(n+2,y1),B(n,y2)在该抛物线上,且y1>y2,请直接写出n的取值范围.