Question

学习了勾股定理以后，有同学提出“在直角三角形中，三边满足a2＋b2＝c2，或许其他的三角形三边也有这样的关系”．让我们来做一个实验！ (1)画出任意一个锐角三角形，量出各边的长度(精确到1 mm)，较短的两条边长分别是a＝________mm；b＝________mm；较长的一条边长c＝________mm．比较：a2＋b2________c2(填“＞”，“＜”或“＝”)． (2)画出任意的一个钝角三角形，量出各边的长度(精确到1 mm)，较短的两条边长分别是a＝________mm；b＝________mm；较长的一条边长c＝________mm．比较：a2＋b2________c2(填“＞”，“＜”或“＝”)． (3)根据以上的操作和结果，对这位同学提出的问题，你猜想的结论是________． 对你猜想a2＋b2与c2的两个关系，利用勾股定理证明你的结论．

Answer 1

答案：
解析：

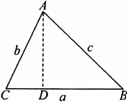
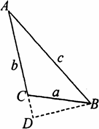
解：(1)(2)略． 　　(3)若△ABC是锐角三角形，则有a2＋b2＞c2； 　　若△ABC是钝角三角形，∠C为钝角，则有a2＋b2＜c2． 　　证明：①当△ABC是锐角三角形时，如图， 　　过点A作AD⊥BC，垂足为D，设CD为x，则有BD＝a－x． 　　根据勾股定理，得AD2＝b2－x2，AD2＝c2－(a－x)2， 　　即b2－x2＝c2－a2＋2ax－x2． 　　∴a2＋b2＝c2＋2ax． 　　∵a＞0，x＞0， 　　∴2ax＞0． 　　∴a2＋b2＞c2． 　　②当△ABC是钝角三角形时，如图， 　　过B作BD⊥AC，交AC的延长线于点D． 　　设CD为x，则有BD2＝a2－x2． 　　根据勾股定理，得(b＋x)2＋a2－x2＝c2． 　　即a2＋b2＋2bx＝c2． 　　∵b＞0，x＞0，∴2bx＞0， 　　∴a2＋b2＜c2．