��Ŀ����
����Ŀ���ۺ���ʵ��
�������֣�
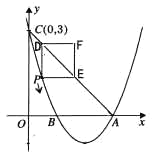
��ͼ1��ͼ2����֪��![]() Ϊ������
Ϊ������![]() �ı�
�ı�![]() ��
��![]() �ϵ�һ�����㣨��
�ϵ�һ�����㣨��![]() ��
��![]() ��
��![]() ���⣩��������
���⣩��������![]() ����
����![]() �ڵ�
�ڵ�![]() ��
��![]() �ڵ�
�ڵ�![]() ��
��![]() �ڵ�
�ڵ�![]() ��
��
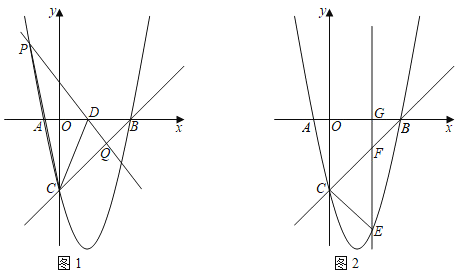
��1����ͼ1������![]() ��
��![]() �ϣ���
�ϣ���![]() ��
��![]() ���⣩�˶�ʱ����֤��
���⣩�˶�ʱ����֤��![]() ��
��
 ����������������
����������������
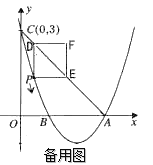
��2����ͼ2������![]() ��
��![]() �ϣ���
�ϣ���![]() ��
��![]() ���⣩�˶�ʱ����ֱ��д���߶�
���⣩�˶�ʱ����ֱ��д���߶�![]() ��
��![]() ��
��![]() ֮���������ϵ��
֮���������ϵ��
�ع�̽����
��3���ڣ�1���������£��ҳ���![]() ��ȵ��߶Σ���˵�����ɣ�
��ȵ��߶Σ���˵�����ɣ�
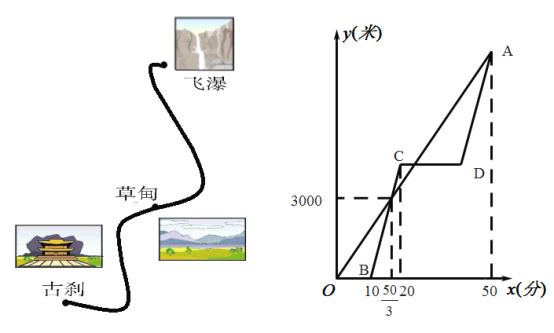
��4����ͼ3������![]() Ϊ����
Ϊ����![]() �ı�
�ı�![]() ��һ�㣬������
��һ�㣬������![]() ����
����![]() �ڵ�
�ڵ�![]() ��
��![]() �ڵ�
�ڵ�![]() ��
��![]() �ڵ�
�ڵ�![]() ����
����![]()
![]() ��
��![]() ����
����![]() _______��
_______��
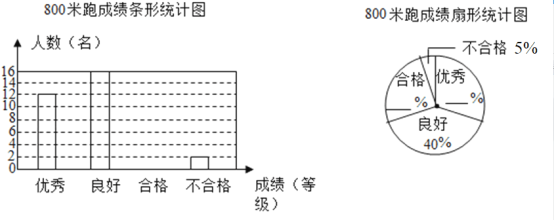
���𰸡���1������������2��![]() ����3��
����3��![]() �����ɼ���������4��
�����ɼ���������4��![]() ��
��
��������
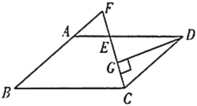
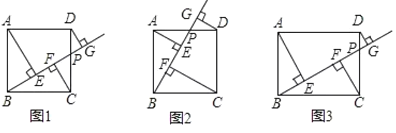
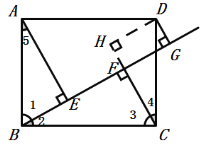
(1)��DH��BG��CF�ӳ����ڵ�H���õ��ı���DGFHΪ���Σ�֤��CF+ DG =CH���跨֤��![]() ���õ�AE=CH������֤�ý��ۣ�
���õ�AE=CH������֤�ý��ۣ�
(2)����(1)�ķ������ɵõ�CF = AE + DG��
(3)����(1)�ķ���֤��![]() ���õ�AE=BF��BE=CF������(1)�Ľ��ۿ����EF= DG��
���õ�AE=BF��BE=CF������(1)�Ľ��ۿ����EF= DG��
(4)��DH��BG��CF�ӳ����ڵ�H���õ��ı���DGFHΪ���Σ��õ� DG= CH- CF��������֪������֤��![]() �������
�������![]() ��
��![]() ����
����![]() ���ɵõ�
���ɵõ�![]() �����
�����![]() ��������ý��ۣ�
��������ý��ۣ�
(1)��D��DH��BG��CF�ӳ����ڵ�H����ͼ��
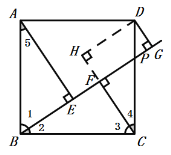
��CF��BG��DG��BG��
���ı���DGFHΪ���Σ�
��DG=HF��
��CF+ DG= CF+ HF =CH��
���ı���ABCDΪ�����Σ���AE��BG��
��AB=CD����ABC=��BCD=��AEB=90![]() ��
��
���5+��1=90![]() ����1+��2=90
����1+��2=90![]() ����2+��3=90
����2+��3=90![]() ����3+��4=90
����3+��4=90![]() ��
��
���5=��4��
��![]() ��
��![]() ��
�У�
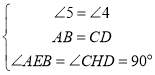 ��
��
��![]() ��
��
��AE=CH��
��AE= CF+ DG��
(2)CF = AE + DG��
����(1)�ķ�������ͼ������֤��CF = AE + DG��
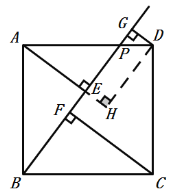
(3)EF= DG���������£���ͼ��

��(1)���5+��1=90![]() ����1+��2=90
����1+��2=90![]() ��
��
���5=��2��
��![]() ��
��![]() ��
�У�
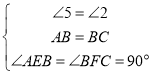 ��
��
��![]() ��
��
��AE=BF��BE=CF��
��EF=BF-BE=AE-CF��
��AE= CF+ DG��
��EF= DG��
(4)��D��DH��BG��CF�ӳ����ڵ�H����ͼ��
��CF��BG��DG��BG��
���ı���DGFHΪ���Σ�
��DG=HF��
��DG= CH- CF��
���ı���ABCDΪ���Σ�AE��BG��CD=2BE=6��
��AB=CD=2BE =6��BE =3����ABC=��BCD=��AEB=90![]() ��
��
��![]() ��
��
��![]() ��
��
�ߡ�ABC=��BCD=��AEB=90![]() ��
��
���5+��1=90![]() ����1+��2=90
����1+��2=90![]() ����2+��3=90
����2+��3=90![]() ����3+��4=90
����3+��4=90![]() ��
��
���5=��4=��2=30![]() ��
��
��![]() ��
��![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() ����
����![]() ��
��
��![]() ��
��
��![]() ��
��