Question

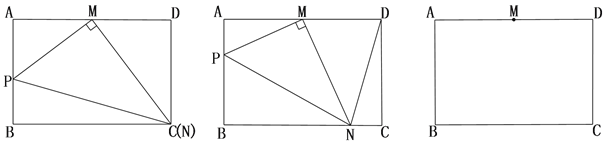
【题目】在矩形ABCD中，AB=4，AD=6，M是AD边的中点，P是射线AB上的一个动点（不与A、B重合），MN⊥PM交射线BC于N点.

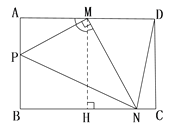
（1）如图1，当点N与点C重合时，求：AP的长；

（2）如图2，在点N的运动过程中，求证： 为定值；

（3）在射线AB上，是否存在点P，使得∽，若存在，求此时AP的长；若不存在，请说明理由.

Answer 1

【答案】（1）AP的长为；

（2）证明见解析；

（3）当时， ∽

【解析】试题分析：（1）易证ΔAMP∽ΔDCM，得，从而可得：

（2）过作于，如图，则，四边形是矩形， ，可证∽，故可得

（3）分和两种情况，利用ΔDCN∽ΔPMN求解即可.

解：（1）∵四边形ABCD是矩形∴

∵

∴

∴∽

∴

∴，

(2)过作于，如图2. ，四边形是矩形，

∵，

∴

又∵ ∴∽

∴

(3）设 （），则

所以

设. ∵，

∴

∴

∴

分两种情况：

（Ⅰ）当时，如图：

∵∽

∴∴∴

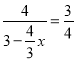
解得： （不合舍去）

（Ⅱ）当时，如图：

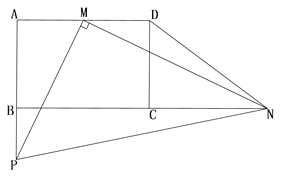
同理：

∴ ，

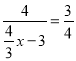解得：

所以当时， ∽