题目内容
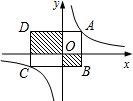
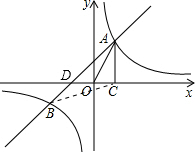
如图,已知反比例函数y1=
(k1>0)与一次函数y2=k2x+1,(k2≠0)相交于A、B两点,AC⊥x轴于点C.若S△OAC=1,tan∠AOC=2
(1)求反比例函数与一次函数的解析式
(2)求S△ABC.

| k1 |
| x |
(1)求反比例函数与一次函数的解析式
(2)求S△ABC.

(1)在Rt△AOC中,tan∠AOC=2,
设AC=2a,则OC=a,
∵S△OAC=
•2a•a=1,即a2=1,
∴a=1,即A(1,2),
将A代入反比例解析式中得:k1=2,即反比例解析式为y1=
;
将A代入一次函数解析式中得:k2=1,即一次函数解析式为y2=x+1;
(2)对于一次函数y2=x+1,令y=0求出x=-1,即OD=1,CD=1+1=2,
联立两函数解析式得:
,
解得:
或
,
∴A(1,2),B(-2,-1),
则S△ABC=S△ADC+S△BDC=
×2×2+
×2×1=3.
设AC=2a,则OC=a,
∵S△OAC=
| 1 |
| 2 |
∴a=1,即A(1,2),
将A代入反比例解析式中得:k1=2,即反比例解析式为y1=
| 2 |
| x |
将A代入一次函数解析式中得:k2=1,即一次函数解析式为y2=x+1;
(2)对于一次函数y2=x+1,令y=0求出x=-1,即OD=1,CD=1+1=2,
联立两函数解析式得:
|
解得:
|
|
∴A(1,2),B(-2,-1),
则S△ABC=S△ADC+S△BDC=
| 1 |
| 2 |
| 1 |
| 2 |


练习册系列答案
相关题目

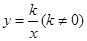 的图象如图3所示,那么函数
的图象如图3所示,那么函数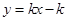 的图象大致是
的图象大致是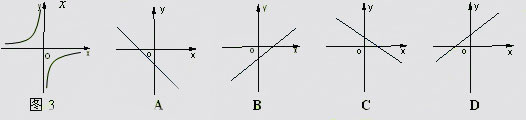
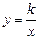 (k≠0)的图象的一个交点为A(-1,2-k2),另—个交点为B,且A、B关于原点O对称,D为OB的中点,过点D的线段OB的垂直平分线与x轴、y轴分别交于C、E.
(k≠0)的图象的一个交点为A(-1,2-k2),另—个交点为B,且A、B关于原点O对称,D为OB的中点,过点D的线段OB的垂直平分线与x轴、y轴分别交于C、E.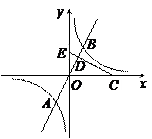





 象似双钩,我们称之为“双钩函数”).给出下列几个命题:
象似双钩,我们称之为“双钩函数”).给出下列几个命题: