题目内容
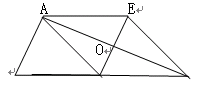
如图,分别以Rt△ABC的直角边AC及斜边AB向外作等边△ACD、等边△ABE.已知∠BAC=30º,EF⊥AB,垂足为F,连结DF.
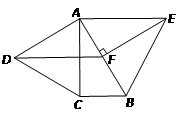
小题1:求证:AC=EF;
小题2:求证:四边形ADFE是平行四边形.
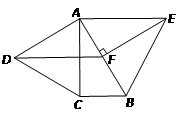
小题1:求证:AC=EF;
小题2:求证:四边形ADFE是平行四边形.
小题1:∵△ABE是等边三角形,
∴AB=AE,∠EAF=60º,
又∵∠BAC=30º,∠ACB=90º,
∴∠ACB=60º, ∴∠EAF=∠ACB,
又∵∠ACB="∠AEF=90" º,∴△ABC≌△EAF.
∴AC=EF.
小题1:∵△ADC是等边三角形,∴AD=AC,∠DAC=60º,
∴AD= EF,
又∵∠CAB=30º,∴∠DAB=90º,
∵∠AEF="90" º,∴AD∥EF
∴四边形ADFE是平行四边形.
小题1:利用三角形全等可证AC=EF。
小题1:一组对边平行且相等的四边形是平行四边形

练习册系列答案
 一本好题口算题卡系列答案
一本好题口算题卡系列答案
相关题目
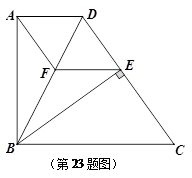
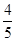 ,S△BCD=
,S△BCD=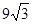 . 求四边形ABCD的周长.
. 求四边形ABCD的周长.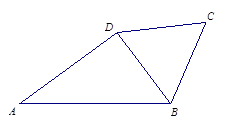
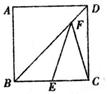
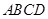 的面积为12,
的面积为12,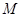 是
是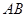 的中点,连接
的中点,连接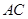 、
、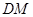 ,则图中阴影部分的面积是 ( ▲ )
,则图中阴影部分的面积是 ( ▲ )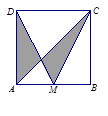
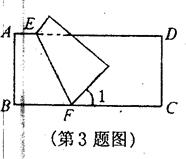
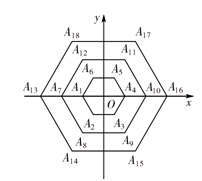
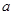 ,求菱形ADCE的周长.(5分)
,求菱形ADCE的周长.(5分)