题目内容
如图:△ABC中,AD是边BC上的中线,过点A作AE∥BC,过点D作DE∥AB与AC、AE分别交于点O、E,连接EC.
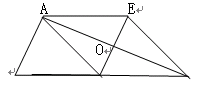
小题1:求证:AD=EC;(4分)
小题2:当∠BAC=90º时,求证:四边形ADCE是菱形;(3分)
小题3:在(2)的条件下,若AB=AO,且OD=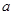 ,求菱形ADCE的周长.(5分)
,求菱形ADCE的周长.(5分)

小题1:求证:AD=EC;(4分)
小题2:当∠BAC=90º时,求证:四边形ADCE是菱形;(3分)
小题3:在(2)的条件下,若AB=AO,且OD=
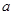 ,求菱形ADCE的周长.(5分)
,求菱形ADCE的周长.(5分)小题1:∵AE∥BC,DE∥AB ∴四边形ABDE是平行四边形(1分)
∴AE=BD ∵D是BC中点 ∴DC=DB(2分)
∴AE="DC" ,AE∥DC ∴四边形ADCE是平行四边形(3分)
∴AD=EC(4分)
小题2:当∠BAC=90º时,AD是Rt△ABC斜边上的中线,(5分)
∴AD=
 (6分)
(6分)∴四边形ADCE是菱形(有一组邻边相等的平行四边形是菱形)(7分)
小题3:∵ADCE是菱形 ∴对角线AC⊥DE且O是DE中点(8分)
∵ABDE是平行四边形 ∴AB="DE" 又已知AB="AO"
∴AO=DE=2DO=2
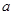 (10分)
(10分)在Rt△AOD中,可求出AD=
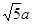 (11分)
(11分)∴菱形ADCE的周长为4
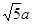 (12分)
(12分)(1)先证四边形ABDE是平行四边形,再证四边形ADCE是平行四边形,即得AD=CE;
(2)由∠BAC=90°,AD上斜边BC上的中线,即得AD=BD=CD,证得四边形ADCE是平行四边形,即证;
(3)利用菱形和平行四边形的性质求出菱形一边的长度,然后再求出它的周长。
(2)由∠BAC=90°,AD上斜边BC上的中线,即得AD=BD=CD,证得四边形ADCE是平行四边形,即证;
(3)利用菱形和平行四边形的性质求出菱形一边的长度,然后再求出它的周长。

练习册系列答案
 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案
相关题目
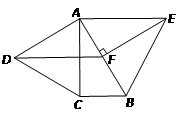
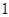 ,按图中所示的规律,用2012个这样的三角形镶嵌而成的四边形的周长是 .
,按图中所示的规律,用2012个这样的三角形镶嵌而成的四边形的周长是 .
 ,则.AC的长为____.
,则.AC的长为____.

 :
:  = 。
= 。
 CG2;③若AF=2DF,则BG=6GF.
CG2;③若AF=2DF,则BG=6GF.

