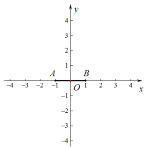Question

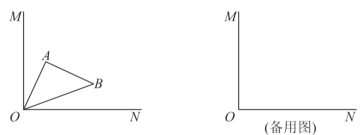
【题目】如图，在平面直角坐标系中，以点为圆心画圆，与轴交于；两点，与轴交于两点，当时，的取值范围是____________.

Answer 1

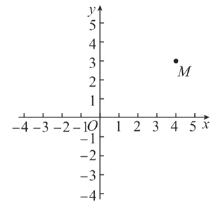
【答案】

【解析】

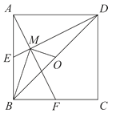
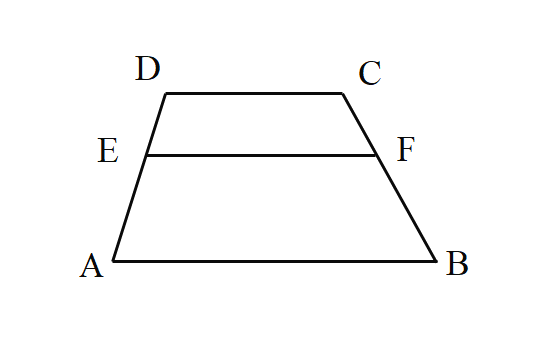
作ME⊥CD于E，MF⊥AB于F，连接MA、MC.当CD=6和CD=时在中求出半径MC,然后在 中可求的值，于是范围可求.

解：如图1，当CD=6时，作ME⊥CD于E，MF⊥AB于F，连接MA、MC，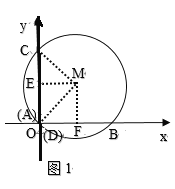

∵，

∴ME=4,MF=3,

∵ME⊥CD, CD=6,

∴CE=3,

∴,

∴MA=MC=5,

∵MF⊥AB,

∴==,

如图2，当CD=时，作ME⊥CD于E，MF⊥AB于F，连接MA、MC，

∵，

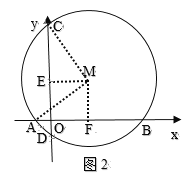
∴ME=4,MF=3,

∵ME⊥CD, CD=,

∴CE=,

∴,

∴MA=MC=8,

∵MF⊥AB,

∴==,

综上所述，当时， .

故答案是：.