Question

【题目】如图，已知线段与点，若在线段上存在点，满足，则称点为线段的“限距点”.

（1）如图，在平面直角坐标系中，若点.

①在中，是线段的“限距点”的是 ；

②点是直线上一点，若点是线段的“限距点”，请求出点横坐标的取值范围.

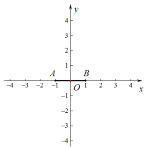
（2）在平面直角坐标系中，点，直线与轴交于点，与轴交于点. 上存在线段的“限距点”，请求出的取值范围.

Answer 1

【答案】（1）①；②；（2）.

【解析】

（1）①已知AB=2，根据勾股定理，结合两点之间的距离公式，即可得到答案；

②根据题意，作出“限距点”的轨迹，结合图形，即可得到答案；

（2）结合（1）的轨迹，作出图像，可分为两种情况进行分析，分别求出两个临界点，即可求出t的取值范围.

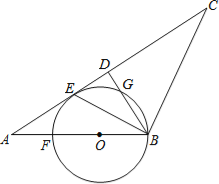
（1）①根据题意，如图：

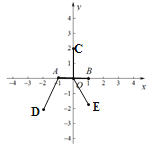
∵点，

∴AB=2，

∵点C为（0，2），点O（0，0）在AB上，

∴OC=AB=2；

∵E为，点O（0，0）在AB上，

∴OE=；

∵点D（）到点A的距离最短，为；

∴线段的“限距点”的是点C、E；

故答案为：C、E.

②由题意直线上满足线段的“限距点”的范围，如图所示.

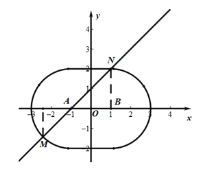
∴点在线段上（包括端点），

∵AM=AB=2，

设点M的坐标为：（n，n）（n<0），

∵，

∴，

∴，

易知，

点横坐标的取值范围为：.

（2）∵与x轴交于点M，与y轴交于点N，

∴令y=0，得；令x=0，得，

∴点M为：（），点N为：（0，）；

如图所示，

此时点M到线段AB的距离为2，

∴，

∴；

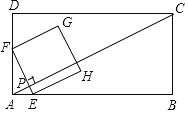
如图所示，AE=AB=2，

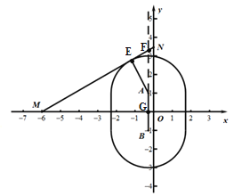
∵∠EMG=∠EAF=30°，

∴，

∵，

∴，，

∴，

∵，AG=1，

∴

解得：；

综上所述：的取值范围为：.