题目内容
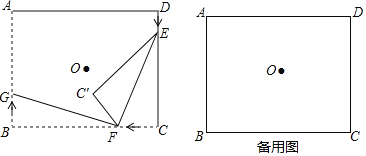
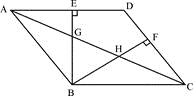
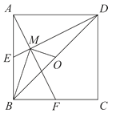
【题目】如图,已知E,F分别为正方形ABCD的边AB,BC的中点,AF与DE交于点M,O为BD的中点,则下列结论:①∠AME=90°;②∠BAF=∠EDB;③∠BMO=90°;④MD=2AM=4EM;⑤![]() .其中正确结论的是( )
.其中正确结论的是( )
A. ①③④B. ②④⑤C. ①③⑤D. ①③④⑤
【答案】D
【解析】
根据正方形的性质可得AB=BC=AD,∠ABC=∠BAD=90°,再根据中点定义求出AE=BF,然后利用“边角边”证明△ABF和△DAE全等,根据全等三角形对应角相等可得∠BAF=∠ADE,然后求出∠ADE+∠DAF=∠BAD=90°,从而求出∠AMD=90°,再根据邻补角的定义可得∠AME=90°,从而判断①正确;根据中线的定义判断出∠ADE≠∠EDB,然后求出∠BAF≠∠EDB,判断出②错误;根据直角三角形的性质判断出△AED、△MAD、△MEA三个三角形相似,利用相似三角形对应边成比例可得![]() ,然后求出MD=2AM=4EM,判断出④正确,设正方形ABCD的边长为2a,利用勾股定理列式求出AF,再根据相似三角形对应边成比例求出AM,然后求出MF,消掉a即可得到AM=
,然后求出MD=2AM=4EM,判断出④正确,设正方形ABCD的边长为2a,利用勾股定理列式求出AF,再根据相似三角形对应边成比例求出AM,然后求出MF,消掉a即可得到AM=![]() MF,判断出⑤正确;过点M作MN⊥AB于N,求出MN、NB,然后利用勾股定理列式求出BM,过点M作GH∥AB,过点O作OK⊥GH于K,然后求出OK、MK,再利用勾股定理列式求出MO,根据正方形的性质求出BO,然后利用勾股定理逆定理判断出∠BMO=90°,从而判断出③正确.
MF,判断出⑤正确;过点M作MN⊥AB于N,求出MN、NB,然后利用勾股定理列式求出BM,过点M作GH∥AB,过点O作OK⊥GH于K,然后求出OK、MK,再利用勾股定理列式求出MO,根据正方形的性质求出BO,然后利用勾股定理逆定理判断出∠BMO=90°,从而判断出③正确.
在正方形ABCD中,AB=BC=AD,∠ABC=∠BAD=90°,
∵E、F分别为边AB,BC的中点,
∴AE=BF=![]() BC,
BC,
在△ABF和△DAE中,
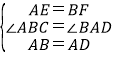 ,
,
∴△ABF≌△DAE(SAS),
∴∠BAF=∠ADE,
∵∠BAF+∠DAF=∠BAD=90°,
∴∠ADE+∠DAF=∠BAD=90°,
∴∠AMD=180°-(∠ADE+∠DAF)=180°-90°=90°,
∴∠AME=180°-∠AMD=180°-90°=90°,故①正确;
∵DE是△ABD的中线,
∴∠ADE≠∠EDB,
∴∠BAF≠∠EDB,故②错误;
∵∠BAD=90°,AM⊥DE,
∴△AED∽△MAD∽△MEA,
∴![]()
∴AM=2EM,MD=2AM,
∴MD=2AM=4EM,故④正确;
设正方形ABCD的边长为2a,则BF=a,
在Rt△ABF中,AF=![]()
∵∠BAF=∠MAE,∠ABC=∠AME=90°,
∴△AME∽△ABF,
∴![]() ,
,
即![]() ,
,
解得AM=![]()
∴MF=AF-AM=![]() ,
,
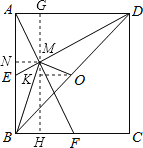
∴AM=![]() MF,故⑤正确;
MF,故⑤正确;
如图,过点M作MN⊥AB于N,
则
![]()
即![]()
解得MN=![]() ,AN=
,AN=![]() ,
,
∴NB=AB-AN=2a-![]() =
=![]() ,
,
根据勾股定理,BM=![]()
过点M作GH∥AB,过点O作OK⊥GH于K,
则OK=a-![]() =
=![]() ,MK=
,MK=![]() -a=
-a=![]() ,
,
在Rt△MKO中,MO=![]()
根据正方形的性质,BO=2a×![]() ,
,
∵BM2+MO2=![]()
![]()
∴BM2+MO2=BO2,
∴△BMO是直角三角形,∠BMO=90°,故③正确;
综上所述,正确的结论有①③④⑤共4个.
故选:D