��Ŀ����
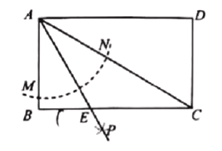
����Ŀ����ͼ��������y=ax2+c��a��0������C��2��0����D��0����1�����㣬����ֱ��y=kx����A��B���㣬ֱ��l����E��0����2����ƽ����x�ᣬ��A��B����ֱ���ֱ��l�Ĵ��ߣ�����ֱ�Ϊ��M��N��

��1����������ߵĽ���ʽ��
��2����֤��AO=AM��
��3��̽����
����k=0ʱ��ֱ��y=kx��x���غϣ������ʱ![]() ��ֵ��
��ֵ��
����˵������kȡ��ֵ��![]() ��ֵ������ͬһ��������
��ֵ������ͬһ��������
���𰸡��⣺��1��y=![]() x2��1
x2��1
��2���������
��3���������
��������
��1���ѵ�C��D��������������߽���ʽ���a��c�����ɵý⡣
��2�����������߽���ʽ�����A�����꣬Ȼ�����AO��AM�ij������ɵ�֤��
��3����k=0ʱ�����AM��BN�ij���Ȼ�����![]() ���㼴�ɵý⣻
���㼴�ɵý⣻
�����A��x1��![]() x12��1����B��x2��
x12��1����B��x2��![]() x22��1����Ȼ���ʾ��
x22��1����Ȼ���ʾ��![]() ����������������ֱ�߽���ʽ������δ֪��y�õ�����x��һԪ���η��̣����ø���ϵ���Ĺ�ϵ��ʾ��x1+x2��x12�������x12+x22��x12x22��Ȼ�������м��㼴�ɵý⡣
����������������ֱ�߽���ʽ������δ֪��y�õ�����x��һԪ���η��̣����ø���ϵ���Ĺ�ϵ��ʾ��x1+x2��x12�������x12+x22��x12x22��Ȼ�������м��㼴�ɵý⡣
�⣺��1����������y=ax2+c��a��0������C��2��0����D��0����1����
��![]() �����
�����![]() ��
��
�������ߵĽ���ʽΪy=![]() x2��1��
x2��1��
��2��֤�������A������Ϊ��m��![]() m2��1����
m2��1����
��![]() ��
��
��ֱ��l����E��0����2����ƽ����x�ᣬ����M��������Ϊ��2��
��AM=![]() m2��1������2��=
m2��1������2��=![]() m2+1��
m2+1��
��AO=AM��
��3����k=0ʱ��ֱ��y=kx��x���غϣ���A��B��x���ϣ�
��AM=BN=0������2��=2��
��![]() ��
��
��kȡ�κ�ֵʱ�����A��x1��![]() x12��1����B��x2��
x12��1����B��x2��![]() x22��1����
x22��1����
��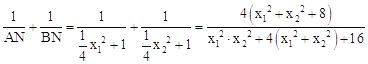 ��
��
����������y�ã�x2��4kx��4=0��
�ɸ���ϵ���Ĺ�ϵ�ã�x1+x2=4k��x1x2=��4��
��x12+x22=��x1+x2��2��2x1x2=16k2+8��x12x22=16��
��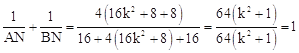 ��
��
������kȡ��ֵ��![]() ��ֵ������ͬһ������1��
��ֵ������ͬһ������1��

 �ִʾ�ƪ��ͬ�����Ĵ��ϵ�д�
�ִʾ�ƪ��ͬ�����Ĵ��ϵ�д�����Ŀ��ij���ͳ���Ͷ��15000Ԫ�ʽ�![]() ��
��![]() ����Ʒ�ƵĿ�Ȫˮ��600�䣬��Ȫˮ�ijɱ��ۺ����ۼ����±���ʾ��
����Ʒ�ƵĿ�Ȫˮ��600�䣬��Ȫˮ�ijɱ��ۺ����ۼ����±���ʾ��
���/���� | �ɱ��ۣ�Ԫ/�䣩 | ���ۼۣ�Ԫ/�䣩 |
AƷ�� | 20 | 32 |
BƷ�� | 35 | 50 |
��1���ô��ͳ��й���![]() ��
��![]() Ʒ�ƿ�Ȫˮ�������䣿
Ʒ�ƿ�Ȫˮ�������䣿
��2��ȫ��������600���Ȫˮ���ó��й���ö�������