题目内容
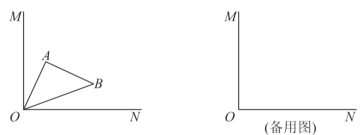
【题目】如图,![]() 于点
于点![]() ,
,![]() 为等腰直角三角形,
为等腰直角三角形,![]() ,当
,当![]() 绕点
绕点![]() 旋转时,记
旋转时,记![]() .
.
(1)过点![]() 作
作![]() 交射线
交射线![]() 于点
于点![]() ,作射线
,作射线![]() 交射线
交射线![]() 于点
于点![]() .
.
①依题意补全图形,求![]() 的度数;
的度数;
②当![]() 时,求
时,求![]() 的长.
的长.
(2)若![]() 上存在一点
上存在一点![]() ,且
,且![]() ,作射线
,作射线![]() 交射线
交射线![]() 于点
于点![]() ,直接写出
,直接写出![]() 长度的最大值.
长度的最大值.
【答案】(1)①见解析, 45°②7;(2)见解析,![]()
【解析】
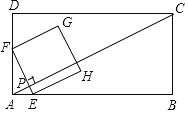
(1)①作![]() 于点H,
于点H,![]() 交
交![]() 的延长线于点
的延长线于点![]() ,证明AHO≌AGB, 即可求得∠ODC的度数;
,证明AHO≌AGB, 即可求得∠ODC的度数;
②延长![]() 交
交![]() 于点
于点![]() ,利用条件可求得AK、OK的长度,于是可求OD的长;
,利用条件可求得AK、OK的长度,于是可求OD的长;
(2)分析可知,点B在以O为圆心,OB为半径的圆上运动(![]() 个圆),所以当PB是圆O的切线时,PQ的值最大,据此可解.
个圆),所以当PB是圆O的切线时,PQ的值最大,据此可解.
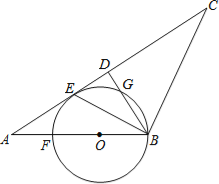
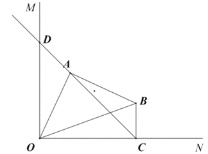
解:(1)①补全图形如图所示,过点![]() 作
作![]() 于点H,
于点H,![]() 交
交![]() 的延长线于点
的延长线于点![]() ,
,

∵![]() ,
,![]() ,
,![]() ,
,
∴∠AGB=∠AHO=∠C =![]() ,
,
∴∠GAH=![]() ,
,
∴∠OAH+∠HAB=∠GAB+∠HAB=![]() ,
,
∴∠OAH =∠GAB, 四边形![]() 为矩形,
为矩形,
∵![]() 为等腰直角三角形,
为等腰直角三角形,
∴OA=AB,
∴AHO≌AGB,
∴AH=AG,
∴四边形![]() 为正方形,
为正方形,
∴∠OCD=45°,
∴∠ODC=45°;
②延长![]() 交
交![]() 于点
于点![]() ,
,

∵![]() ,OA=5,
,OA=5,
∴AK=4,
∴OK=3,
∵∠ODC=45°,
∴DK=AK=4
∴![]() ;
;
(2)如图,

∵![]() 绕点
绕点![]() 旋转,
旋转,![]()
∴点B在以O为圆心,OB为半径的圆上运动(![]() 个圆),
个圆),
∴当PB是圆O的切线时,PQ的值最大,
∵![]()
∴![]()
∴∠OPB=45°,
∴ OQ=OP=10,
∴![]() .
.
∴![]() 长度的最大值是
长度的最大值是![]() .
.

练习册系列答案
相关题目