题目内容

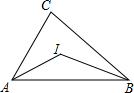
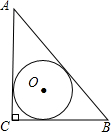
如图在△ABC中∠A=70°，⊙O截△ABC的三条边所得的弦长相等，则∠BOC=（　　）
A．140°B．135°C．130°D．125°

∵△ABC中∠A=70°，⊙O截△ABC的三条边所得的弦长相等，
∴O到三角形三条边的距离相等，即O是△ABC的内心，
∴∠1=∠2，∠3=∠4，∠1+∠3=
1
2
（180°-∠A）=
1
2
（180°-70°）=55°，
∴∠BOC=180°-（∠1+∠3）=180°-55°=125°．
故选D．
练习册系列答案
相关题目
如图，点I是△ABC的内切圆的圆心，若∠BIC=130°，则∠A的度数是______．
我们给出如下定义：三角形三条中线的交点称为三角形的重心．一个三角形有且只有一个重心．可以证明三角形的重心与顶点的距离等于它与对边中点的距离的两倍．
可以根据上述三角形重心的定义及性质知识解答下列问题：
如图，∠B的平分线BE与BC边上的中线AD互相垂直，并且BE=AD=4
（1）猜想AG与GD的数量关系，并说明理由；
（2）求△ABC的三边长．
某地有四个村庄E，F，G，H（其位置如图所示），现拟建一个电视信号中转站，信号覆盖的范围是以发射台为圆心的圆形区域．为了使这四个村庄的居民都能接收到电视信号，且使中转站所需发射功率最小（圆形区域半径越小，所需功率越小），此中转站应建在（　　）
A．线段HF的中点处B．△GHE的外心处
C．△HEF的外心处D．△GEF的外心处
在△ABC中，∠A=70°，若O为△ABC的外心，则∠BOC=______度；若O为△ABC的内心，则∠BOC=______度．
解答题：
（1）设互为补角的两个角的差为60°，求较小角的余角．
（2）设一个角的补角是这个角的余角的5倍，求这个角的度数．
（3）如图，∠1=∠2，∠EMB=55°，试求∠DNF的度数．

（4）如图，△ABC三个顶点分别表示三个小区，AB，BC，AC是连接三个小区的已有自来水管道，某工程队现在要△ABC在内部（包括边上）建一个自来水公司M，M到AB，BC，AC的距离和计为L，已知AB=4，BC=5，AC=6，问自来水供应M在哪个位置，工程对才有最大的经济效益（即L最小）
如图，Rt△ABC中，∠C=90°，⊙O为△ABC的内切圆，若AC=6，BC=8，求⊙O半径．
点O是△ABC内一点，且O到三边的距离相等，∠A=62°，则∠BOC=______°．
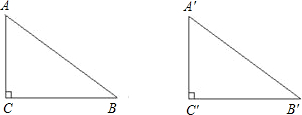在Rt△ABC和Rt△A′B′C′中，∠C=∠C′=90°，如图，那么下列各条件中，不能使Rt△ABC≌Rt△A′B′C′的是（　　）
A．AB=A′B′=5，BC=B′C′=3B．AB=B′C′=5，∠A=∠B′=40°
C．AC=A′C′=5，BC=B′C′=3D．AC=A′C′=5，∠A=∠A′=40°

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网