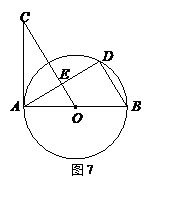题目内容
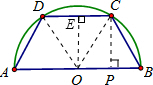
(2011四川泸州,17,3分)如图,半径为2的圆内接等腰梯形ABCD,它的下底AB是圆的直径,上底CD的端点在圆周上,则该梯形周长的最大值是 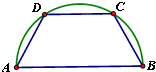

18.
答案为:10
根据圆心为O,则OA=OB=OC=OD=2,设腰长为x,设上底长是2b,利用勾股定理得出,则x2-(2-b)2=R2-b2=CP2,再利用二次函数最值求出即可.
解:圆心为O,连接OD,OC,过O作OE⊥CD,过C作CP⊥OB,
∴E为DC的中点,DE=CE=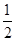 CD=b,
CD=b,
∵等腰梯形ABCD,
∴DC∥AB,OE⊥CD,
∴OE⊥AB,
∴∠CEO=∠EOP=∠OPC=90°,
∴四边形EOPC为矩形,
∴EC=OP,
则OA=OB=OC=OD=2,设腰长为x,
设上底长是2b,过C作直径的垂线,垂足是P,
则CP2=OC2-OP2=CB2-PB2,
即x2-(2-b)2=22-b2,
整理得b=2-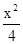 ,
,
所以y=4+2x+2b=4+2x+4-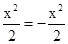 +2x+8,
+2x+8,
∴该梯形周长的最大值是:
故答案为:10.
根据圆心为O,则OA=OB=OC=OD=2,设腰长为x,设上底长是2b,利用勾股定理得出,则x2-(2-b)2=R2-b2=CP2,再利用二次函数最值求出即可.
解:圆心为O,连接OD,OC,过O作OE⊥CD,过C作CP⊥OB,
∴E为DC的中点,DE=CE=
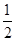 CD=b,
CD=b,∵等腰梯形ABCD,
∴DC∥AB,OE⊥CD,
∴OE⊥AB,
∴∠CEO=∠EOP=∠OPC=90°,
∴四边形EOPC为矩形,
∴EC=OP,

则OA=OB=OC=OD=2,设腰长为x,
设上底长是2b,过C作直径的垂线,垂足是P,
则CP2=OC2-OP2=CB2-PB2,
即x2-(2-b)2=22-b2,
整理得b=2-
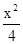 ,
,所以y=4+2x+2b=4+2x+4-
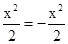 +2x+8,
+2x+8,∴该梯形周长的最大值是:

故答案为:10.

练习册系列答案
 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
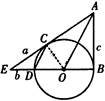
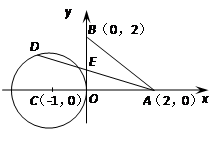

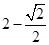 D.
D.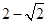
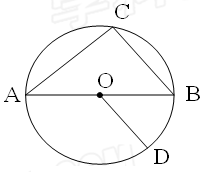
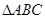 中,
中,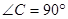 ,且两边长分别为4
,且两边长分别为4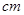 和5
和5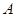 为圆心,3
为圆心,3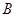 为圆心,2
为圆心,2
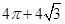 B.
B.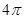 C.
C.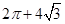 D.
D.
 和⊙
和⊙ 相交于
相交于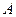 、
、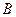 两点,过点
两点,过点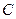 ,过点
,过点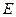 、
、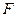 ,
,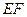 与
与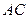 相交于点
相交于点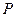 ,
, 1)求证:
1)求证: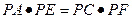 ;
;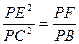 ;
;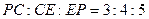 时,求
时,求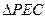 与
与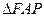 的面积的比值。
的面积的比值。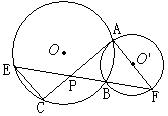
 是⊙
是⊙ 的直径,AC与⊙
的直径,AC与⊙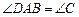 .
.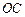 ∥
∥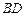 ;
;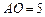 ,
,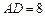 ,求线段CE的长.
,求线段CE的长.