题目内容
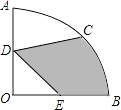
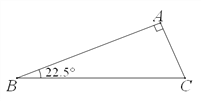
【题目】如图,在平面直角坐标系中,O为坐标原点, ![]() 的圆心坐标为
的圆心坐标为![]() ,半径为
,半径为![]() 函数
函数![]() 的图象与x轴交于点A,与y轴交于点B,点P为线段AB上一动点.
的图象与x轴交于点A,与y轴交于点B,点P为线段AB上一动点.
![]() 连接CO,求证:
连接CO,求证: ![]() ;
;
![]() 若
若![]() 是等腰三角形,求点P的坐标;
是等腰三角形,求点P的坐标;
![]() 当直线PO与
当直线PO与![]() 相切时,求
相切时,求![]() 的度数;当直线PO与
的度数;当直线PO与![]() 相交时,设交点为E、F,点M为线段EF的中点,令
相交时,设交点为E、F,点M为线段EF的中点,令![]() ,求s与t之间的函数关系,并写出t的取值范围.
,求s与t之间的函数关系,并写出t的取值范围.

【答案】答案见解析.
【解析】试题分析:(1)利用一次函数与坐标轴交点求法得出A,B坐标,进而得出∠COG=45°,∠AOD=45°,即可得出答案;
(2)利用①当OP=OA时,②当OP=PA时,③当AP=AO时分别得出P点坐标;
(3)利用切线的性质以及点的坐标性质得出∠POA的度数;根据已知得出△COM∽△POD,进而得出MOPO=CODO,即可得出s与t的关系,进而求出t的取值范围.
试题解析: ![]() 延长CO交AB于D,过点C作
延长CO交AB于D,过点C作![]() 轴于点G,
轴于点G,
![]() 直线AB的函数关系式是
直线AB的函数关系式是![]() 易得
易得![]() ,
,
![]() ,
,
又![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,即
,即![]() ;
;
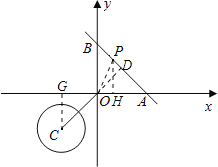
![]() 要使
要使![]() 为等腰三角形,
为等腰三角形,
![]() 当
当![]() 时,此时点P与点B重合,
时,此时点P与点B重合, ![]() 点P坐标为
点P坐标为![]() ;
;
![]() 当
当![]() 时,由
时,由![]() 点P恰好是AB的中点,
点P恰好是AB的中点, ![]() 点P坐标为
点P坐标为![]() ;
;
![]() 当
当![]() 时,则
时,则![]() ,过点P作
,过点P作![]() 交于点H,
交于点H,
在![]() 中,易得
中,易得![]() 点坐标为
点坐标为![]() ,
,
综上所述, ![]() 、
、![]() 、
、![]() ;
;
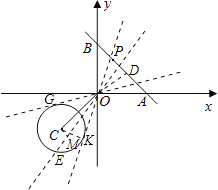
![]() 当直线PO与
当直线PO与![]() 相切时,设切点为K,连接CK,则
相切时,设切点为K,连接CK,则![]() ,
,
由点C的坐标为![]() ,易得
,易得![]() ,
,
又![]() 的半径为
的半径为![]() ,
,
![]() ,又
,又![]() ,
,
同理可求出![]() 的另一个值为
的另一个值为![]() ,
,
![]() 等于
等于![]() 或
或![]() ,
,
![]() 为EF的中点,
为EF的中点, ![]() ,
,
又![]() ,
,
![]() ∽
∽![]() ,
,
![]() ,即
,即![]() ,
,
![]() ,
,
当PO过圆心C时, ![]() ,
,
即![]() ,也满足
,也满足![]()

练习册系列答案
相关题目