Question

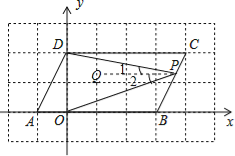
【题目】(10分)如图，在直角坐标系xOy中，A(﹣1，0)，B(3，0)，将A，B同时分别向上平移2个单位，再向右平移1个单位，得到的对应点分别为D，C，连接AD，BC.

(1)直接写出点C，D的坐标：C ，D ；

(2)四边形ABCD的面积为 ；

(3)点P为线段BC上一动点(不含端点)，连接PD，PO.求证：∠CDP+∠BOP=∠OPD.

Answer 1

【答案】(1)(4，2)，(0，2)；(2)8；(3)见解析

【解析】试题分析：（1）根据C、D两点在坐标系中的位置即可得出此两点坐标；

（2）先判断出四边形ABCD是平行四边形，再求出其面积即可；

（3）过点P作PQ∥AB，故可得出CD∥PQ，AB∥PQ，由平形线的性质即可得出结论．

解：（1）由图可知，C（4，2），D（0，2）．

故答案为：（4，2），（0，2）；

（2）∵线段CD由线段BA平移而成，

∴AB∥CD，AB=CD，

∴四边形ABCD是平行四边形，

∴S平行四边形ABCD=4×2=8．

故答案为：8；

（3）证明：如图，过点P作PQ∥AB，

∵CD∥AB，

∴CD∥PQ，AB∥PQ，

∴∠CDP=∠1，∠BOP=∠2，

∴∠CDP+∠BOP=∠1+∠2=∠OPD．