题目内容
【题目】(1)计算(2a+1)2﹣(2a+1)(﹣1+2a);
(2)用乘法公式计算:20022﹣2001×2003;
(3)解不等式组: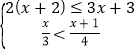 ,并把解集在数轴上表示出来;
,并把解集在数轴上表示出来;
(4)解方程组: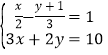 .
.
【答案】(1)4a+2;(2)1;(3)1≤x<3;(4)![]() .
.
【解析】分析(1)原式第一项利用完全平方公式展开,第二项利用平方差公式化简,去括号合并即可得到结果;
(2)原式变形后,利用平方差公式计算即可得到结果;
(3)分别求出不等式组中两不等式的解集,找出解集的公共部分即可;
(4)方程组变形后,利用加减消元法求出解即可.
:(1)原式=4a2+4a+1﹣4a2+1
=4a+2;
(2)原式=20022﹣(2002﹣1)×(2002+1)=20022﹣20022+1=1;
(3)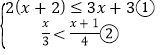 ,
,
由①得:x≥1;
由②得:x<3,
则不等式组的解集为 1≤x<3,
把解集在数轴上表示出来为:![]()
(4)方程组整理得: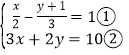 ,
,
①+②得:6x=18,即 x=3,
将 x=3 代入①得:y=![]() ,
,
则方程组的解为![]() .
.

练习册系列答案
 小题狂做系列答案
小题狂做系列答案
相关题目