Question

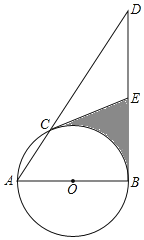
【题目】如图，△ABC内接于⊙O，AB为⊙O的直径，过点A作⊙O的切线交BC的延长线于点E，在弦BC上取一点F，使AF＝AE，连接AF并延长交⊙O于点D．

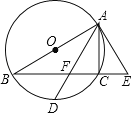
（1）求证：∠B＝∠CAD；

（2）若CE＝2，∠B＝30°，求AD的长．

Answer 1

【答案】（1）详见解析；（2）6．

【解析】

（1）根据切线的性质和圆周角的定理得∠BAE＝∠ACB＝90°，进而求得∠B＝∠CAE，根据等腰三角形三线合一的性质得出∠CAD＝∠CAE，即可证得结论；

（2）连接BD，易证得∠BAD＝30°，解直角三角形求得AE，进而求得AB，然后即可求得AD．

（1）证明：∵AE是⊙O的切线，

∴∠BAE＝90°，

∵AB为⊙O的直径，

∴∠ACB＝90°，

∴∠BAC+∠CAE＝90°，∠BAC+∠B＝90°，

∴∠B＝∠CAE，

∵AF＝AE，∠ACB＝90°，

∴∠CAD＝∠CAE．

∴∠B＝∠CAD；

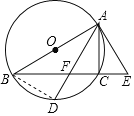
（2）解：连接BD．

∵∠ABC＝∠CAD＝∠CAE＝30°，

∴∠DAE＝60°，

∵∠BAE＝90°，

∴∠BAD＝30°，

∵AB是直径，

∴∠ADB＝90°，

∴cos∠BAD＝，

∴＝，

∵∠ACE＝90°，∠CAE＝30°，CE＝2，

∴AE＝2CE＝4，

∵∠BAE＝90°，∠ABC＝30°，

∴cot∠ABC＝，即＝，

∴AB＝4，

∴＝，

∴AD＝6．