Ő‚ńŅńŕ»›
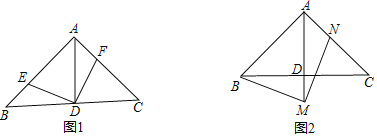
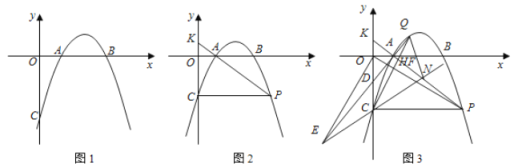
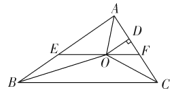
°ĺŐ‚ńŅ°Ņ»ÁÕľ£¨Ň◊őÔŌŖy=ax2+(4a©Ā1)x©Ā4”Žx÷ŠĹĽ”ŕĶ„A°ĘB£¨”Žy÷ŠĹĽ”ŕĶ„C£¨«“OC=2OB£¨Ķ„Dő™ŌŖ∂őOB…Ō“Ľ∂ĮĶ„(≤Ľ”ŽĶ„B÷ōļŌ)£¨ĻżĶ„D◊ųĺō–őDEFH£¨Ķ„H°ĘF‘ŕŇ◊őÔŌŖ…Ō£¨Ķ„E‘ŕx÷Š…Ō£ģ
£®1£©«ůŇ◊őÔŌŖĶńĹ‚őŲ Ĺ£Ľ
£®2£©ĶĪĺō–őDEFHĶń÷‹≥§◊Óīů Ī£¨«ůĺō–őDEFHĶń√śĽż£Ľ
£®3£©‘ŕ£®2£©ĶńŐűľĢŌ¬£¨ĺō–őDEFH≤Ľ∂Į£¨ĹęŇ◊őÔŌŖ—ō◊Ňx÷ŠŌÚ◊ů∆Ĺ“∆młŲĶ•őĽ£¨Ň◊őÔŌŖ”Žĺō–őDEFHĶńĪŖĹĽ”ŕĶ„M°ĘN£¨Ń¨Ĺ”M°ĘN£ģ»ŰMN«°ļ√∆Ĺ∑÷ĺō–őDEFHĶń√śĽż£¨«ůmĶń÷Ķ£ģ

°ĺīūįł°Ņ£®1£©y=![]() x2+x©Ā4£Ľ£®2£©10£Ľ£®3£©mĶń÷Ķő™
x2+x©Ā4£Ľ£®2£©10£Ľ£®3£©mĶń÷Ķő™![]() £ģ
£ģ
°ĺĹ‚őŲ°Ņ
£®1£©Ō»«ů≥ŲĶ„CĶń◊ÝĪÍ£¨”…OC£Ĺ2OB£¨Ņ…Õ∆≥ŲĶ„B◊ÝĪÍ£¨ĹęĶ„B◊ÝĪÍīķ»Žy£Ĺax2£ę£®4a©Ā1£©x©Ā4Ņ…«ů≥ŲaĶń÷Ķ£¨ľīŅ…–ī≥ŲŇ◊őÔŌŖĶńĹ‚őŲ Ĺ£Ľ
£®2£©…ŤĶ„D◊ÝĪÍő™£®x£¨0£©£¨”√ļ¨xĶńīķ ż ĹĪŪ ĺ≥Ųĺō–őDEFHĶń÷‹≥§£¨”√ļĮ żĶńňľŌŽ«ů≥Ų»°∆š◊Óīů÷Ķ ĪxĶń÷Ķ£¨ľī«ů≥ŲĶ„DĶń◊ÝĪÍ£¨ĹÝ“Ľ≤ĹŅ…«ů≥Ųĺō–őDEFHĶń√śĽż£Ľ
£®3£©»ÁÕľ£¨Ń¨Ĺ”BH£¨EH£¨DF£¨…ŤEH”ŽDFĹĽ”ŕĶ„G£¨ĻżĶ„G◊ųBHĶń∆Ĺ––ŌŖ£¨ĹĽED”ŕM£¨ĹĽHF”ŕĶ„N£¨‘Ú÷ĪŌŖMNĹęĺō–őDEFHĶń√śĽż∑÷≥…ŌŗĶ»ĶńŃĹįŽ£¨“ņīő«ů≥Ų÷ĪŌŖBH£¨MNĶńĹ‚őŲ Ĺ£¨‘Ŕ«ů≥ŲĶ„MĶń◊ÝĪÍ£¨ľīŅ…Ķ√≥ŲmĶń÷Ķ£ģ
Ĺ‚£ļ£®1£©‘ŕŇ◊őÔŌŖy£Ĺax2£ę(4a©Ā1)x©Ā4÷–£¨
ĶĪx£Ĺ0 Ī£¨y£Ĺ©Ā4£¨
°ŗC(0£¨©Ā4)£¨
°ŗOC£Ĺ4£ģ
°ŖOC£Ĺ2OB£¨
°ŗOB£Ĺ2£¨
°ŗB(2£¨0)£¨
ĹęB(2£¨0)īķ»Žy£Ĺax2£ę(4a©Ā1)x©Ā4£¨Ķ√£ļa£Ĺ![]() £¨
£¨
°ŗŇ◊őÔŌŖĶńĹ‚őŲ Ĺő™y£Ĺ![]() x2£ęx©Ā4£Ľ
x2£ęx©Ā4£Ľ
£®2£©…ŤĶ„D◊ÝĪÍő™(x£¨0)£ģ
°ŖňńĪŖ–őDEFHő™ĺō–ő£¨
°ŗH(x£¨![]() x2£ęx©Ā4)£ģ
x2£ęx©Ā4)£ģ
°Ŗy£Ĺ![]() x2£ęx©Ā4£Ĺ
x2£ęx©Ā4£Ĺ![]() (x£ę1)2©Ā
(x£ę1)2©Ā![]() £¨
£¨
°ŗŇ◊őÔŌŖ∂‘≥∆÷Šő™x£Ĺ©Ā1£¨
°ŗĶ„HĶĹ∂‘≥∆÷ŠĶńĺŗņŽő™x£ę1£¨
”…∂‘≥∆–‘Ņ…÷™DE£ĹFH£Ĺ2x£ę2£¨
°ŗĺō–őDEFHĶń÷‹≥§C£Ĺ2(2x£ę2)£ę2(©Ā![]() x2©Āx£ę4)£Ĺ©Āx2£ę2x£ę12£Ĺ©Ā(x©Ā1)2£ę13£¨
x2©Āx£ę4)£Ĺ©Āx2£ę2x£ę12£Ĺ©Ā(x©Ā1)2£ę13£¨
°ŗĶĪx£Ĺ1 Ī£¨ĺō–őDEFH÷‹≥§»°◊Óīů÷Ķ13£¨
°ŗīň ĪH(1£¨©Ā![]() )£¨
)£¨
°ŗHF£Ĺ2x£ę2£Ĺ4£¨DH£Ĺ![]() £¨
£¨
°ŗSĺō–őDEFH£ĹHFDH£Ĺ4°Ń![]() £Ĺ10£Ľ
£Ĺ10£Ľ
£®3£©»ÁÕľ£¨
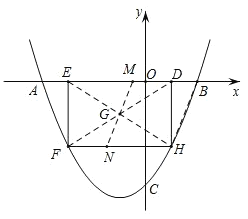
ѨŔBH£¨EH£¨DF£¨…ŤEH”ŽDFĹĽ”ŕĶ„G£¨
ĻżĶ„G◊ųBHĶń∆Ĺ––ŌŖ£¨ĹĽED”ŕM£¨ĹĽHF”ŕĶ„N£¨‘Ú÷ĪŌŖMNĹęĺō–őDEFHĶń√śĽż∑÷≥…ŌŗĶ»ĶńŃĹįŽ£¨
”…£®2£©÷™£¨Ň◊őÔŌŖ∂‘≥∆÷Šő™x£Ĺ©Ā1£¨H(1£¨©Ā![]() )£¨
)£¨
°ŗG(©Ā1£¨©Ā![]() )£¨
)£¨
…Ť÷ĪŌŖBHĶńĹ‚őŲ Ĺő™y£Ĺkx£ęb£¨
ĹęĶ„B(2£¨0)£¨H(1£¨©Ā![]() )īķ»Ž£¨
)īķ»Ž£¨
Ķ√£ļ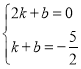 £¨Ĺ‚Ķ√£ļ
£¨Ĺ‚Ķ√£ļ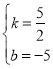 £¨
£¨
°ŗ÷ĪŌŖBHĶńĹ‚őŲ Ĺő™y£Ĺ![]() x©Ā5£¨
x©Ā5£¨
°ŗŅ……Ť÷ĪŌŖMNĶńĹ‚őŲ Ĺő™y£Ĺ![]() x£ęn£¨
x£ęn£¨
ĹęĶ„(©Ā1£¨©Ā![]() )īķ»Ž£¨Ķ√n£Ĺ
)īķ»Ž£¨Ķ√n£Ĺ![]() £¨
£¨
°ŗ÷ĪŌŖMNĶńĹ‚őŲ Ĺő™y£Ĺ![]() x£ę
x£ę![]() £¨
£¨
ĶĪy£Ĺ0 Ī£¨x£Ĺ©Ā![]() £¨
£¨
°ŗM(©Ā![]() £¨0)£ģ
£¨0)£ģ
°ŖB(2£¨0)£¨
°ŗĹęŇ◊őÔŌŖ—ō◊Ňx÷ŠŌÚ◊ů∆Ĺ“∆![]() łŲĶ•őĽ£¨Ň◊őÔŌŖ”Žĺō–őDEFHĶńĪŖĹĽ”ŕĶ„M°ĘN£¨
łŲĶ•őĽ£¨Ň◊őÔŌŖ”Žĺō–őDEFHĶńĪŖĹĽ”ŕĶ„M°ĘN£¨
ѨŔM°ĘN£¨‘ÚMN«°ļ√∆Ĺ∑÷ĺō–őDEFHĶń√śĽż£¨
°ŗmĶń÷Ķő™![]() £ģ
£ģ

 ÓľŔ◊ų“Ķ ÓľŔŅžņ÷Ń∑őųį≤≥Ųįś…ÁŌĶŃ–īūįł
ÓľŔ◊ų“Ķ ÓľŔŅžņ÷Ń∑őųį≤≥Ųįś…ÁŌĶŃ–īūįł