Question

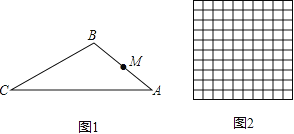
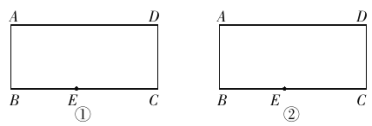
【题目】在图①②中，点E在矩形ABCD的边BC上，且BE=AB，现要求仅用无刻度的直尺分别按下列要求画图．[保留画(作)图痕迹，不写画(作)法]

（1）在图①中，画∠BAD的平分线；

（2）在图②中，画∠BCD的平分线．

Answer 1

【答案】（1）见解析；（2）见解析

【解析】

(1)连接AE，等边对等角可得∠BAE=∠BEA=45，再根据平行线的性质即可得到AE是∠BAD的平分线；
(2)连接矩形ABCD的对角线，交于点O，可得AO=CO，再连接EO并延长，交BC于P，根据△APO≌△CEO，可得AP=CE，得到四边形AECP为平行四边形，得到∠ECP=∠BEA=45，即可得到CP是∠BCD的平分线．

(1)如图所示，AE即为所求；

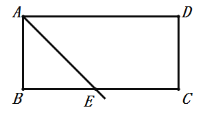
∵点E在矩形ABCD的边BC上，且BE=AB，

∴∠B=90，∠BAE=∠BEA=45，

∵AD∥BC，

∴∠DAE=∠BEA=45，

∴∠DAE=∠BAE，

∴AE是∠BAD的平分线；

(2)如图所示，CP即为所求；

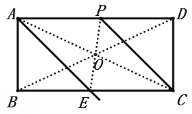
∵四边形ABCD是矩形，

∴AP∥EC，

∴∠PAO=∠ECO，

点O是矩形ABCD对角线的交点，

∴AO=CO，

∵∠POA=∠EOC，

∴△APO≌△CEO，

∴AP=CE，

又∵AP∥EC，

∴四边形AECP为平行四边形，

∴AE∥PC，

∴∠ECP=∠BEA=45，

∴CP是∠BCD的平分线．