Question

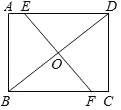
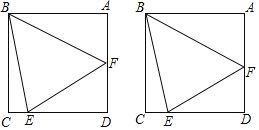
【题目】如图，边长为1的正方形ABCD中，点E、F分别在边CD、AD上，连接BE、BF、EF，且有AF+CE＝EF．

（1）求(AF+1)(CE+1)的值；

（2）探究∠EBF的度数是否为定值，并说明理由；

Answer 1

【答案】（1）2；（2）∠EBF的度数为定值，理由见解析

【解析】

（1）设CE=x，AF=y，先根据EF2=DE2+DF2推出xy+x+y=1，再用含和的式子表示并整体代值即得；

（2）将绕点B顺时针旋转90°得到，证明，进而得出∠EBF=∠ABF+∠CBE即得．

解：（1）设CE=x，AF=y，则DE=1﹣x，DF=1﹣y，∵AF+CE=EF，

∴EF=x+y，∵四边形ABCD是矩形，∴∠D=90°，∴，

∴

∴xy+x+y＝1

∴；

（2）∠EBF的度数为定值，理由如下：

如图1，将绕点B顺时针旋转90°得到，此时AB与CB重合．

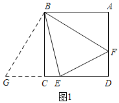
由旋转可得AB=BC，BF=BG，∠ABF=∠CBG，∠BCG=∠A=90°．

∴∠BCG+∠BCD=90°+90°=180°．∴点G、C、E在同一条直线上．

∵AF+CE=EF=CG+CE=EG，

∵BE=BE

∴

∴∠EBF=∠EBG=∠CBG+∠CBE=∠ABF+∠CBE，

∵∠ABC=90°，∴∠EBF=45°

∴∠EBF的度数为定值；