题目内容
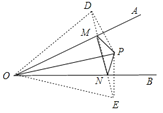
【题目】如图,∠AOB=30°,内有一点P且OP=![]() ,若M、N为边OA、OB上两动点,那么△PMN的周长最小为( )
,若M、N为边OA、OB上两动点,那么△PMN的周长最小为( )

A. ![]() B. 6 C.
B. 6 C. ![]() D.
D. ![]()
【答案】D
【解析】作P关于OA的对称点D,作P关于OB的对称点E,连接DE交OA于M,交OB于N,连接PM,PN,则此时△PMN的周长最小,此时周长最小值等于DE,
因为P,D关于OA对称,
所以OD=OP, ∠DOM=∠POM,
因为P,E关于OB对称,
所以OE=OP, ∠EON=∠PON,
因为∠DOE=∠DOM+∠POM+∠PON+∠EON=2∠MON, ∠AOB=30°,
所以∠DOE=2∠AOB=60°,
所以△DOE是等边三角形,
所以DE=OD=OP=![]() ,
,
所以△PMN的周长最小是![]() ,故选D.
,故选D.

练习册系列答案
 计算高手系列答案
计算高手系列答案
相关题目