题目内容
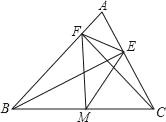
【题目】如图,在△ABC中,CF⊥AB于F,BE⊥AC于E,M为BC的中点.
(1)若EF=3,BC=8,求△EFM的周长;
(2)若∠ABC=50°,∠ACB=60°,求∠EMF的度数.
【答案】(1)11;(2)40°.
【解析】
(1)根据直角三角形斜边上的中线等于斜边的一半可得EM=MC=![]() BC,MF=MB=
BC,MF=MB= ![]() BC,然后根据三角形的周长的定义列式计算即可得解;
BC,然后根据三角形的周长的定义列式计算即可得解;
(2)根据等边对等角求出,∠ABC=∠MFB,∠ACB=∠MEC,再根据三角形的内角和定理求出∠BMF, ∠EMC,然后利用平角等于180°列式计算即可得解.
(1)∵CF⊥AB于F, M为BC的中点,∴ME=MC=![]() BC=
BC=![]() ×8=4,同理MF=MB=
×8=4,同理MF=MB= ![]() BC=
BC=![]() ×8=4,∴△EFM的周长=4+4+3=11;
×8=4,∴△EFM的周长=4+4+3=11;
(2)∵MF=MB,∴∠ABC=∠MFB=50°,同理∠ACB=∠MEC=60°,∴∠BMF=180°-50°-50°=80°,∠EMC=180°-60°-60°=60°,∴∠EMF=180°-80°-60°=40°.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
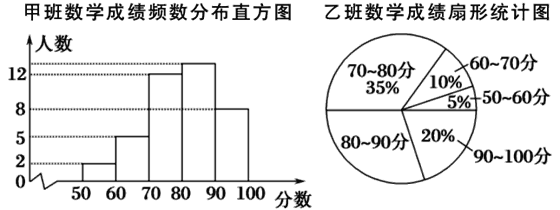
【题目】光明中学八年级甲、乙、丙三个班中,每班的学生人数都为40名,某次数学考试的成绩统计如图:(每组分数含最小值,不含最大值)
丙班数学成绩频数统计表
分数 | 50~60 | 60~70 | 70~80 | 80~90 | 90~100 |
人数 | 1 | 4 | 15 | 11 | 9 |
根据上图及统计表提供的信息,则80~90分这一组人数最多的班是________