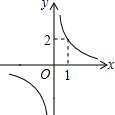题目内容
如图,直线y=kx+k(k≠0)与双曲线y=
交于C、D两点,与x轴交于点A.
(1)求n的取值范围和点A的坐标;
(2)过点C作CB⊥y轴,垂足为B,若S△ABC=4,求双曲线的解析式;
(3)在(1)(2)的条件下,若AB=
,求点C和点D的坐标,并根据图象直接写出反比例函数的值小于一次函数的值时,自变量x的取值范围.

| n+1 |
| x |
(1)求n的取值范围和点A的坐标;
(2)过点C作CB⊥y轴,垂足为B,若S△ABC=4,求双曲线的解析式;
(3)在(1)(2)的条件下,若AB=
| 17 |

(1)由图象得:n+1<0,
解得:n<-1,
由y=kx+k,令y=0,解得:x=-1,
则A坐标为(-1,0);
(2)设C(a,b),
∵S△ABC=
a•(-b)=4,
∴ab=-8,
∵点C在双曲线上,
∴y=-
;
(3)∵CB⊥y轴,∴B(0,b),
在Rt△AOB中,AB=
,OA=1,
根据勾股定理得:OB=4,
∴B(0,-4),
∴C(2,-4),
将C代入直线y=kx+k中,得:2k+k=-4,即k=-
,
∴直线AC解析式为y=-
x-
,
联立直线与反比例解析式得:
,
解得:
或
,
∴D(-3,
),
则由图象可得:当x<-3或0<x<2时,反比例函数的值小于一次函数的值.
解得:n<-1,
由y=kx+k,令y=0,解得:x=-1,
则A坐标为(-1,0);
(2)设C(a,b),
∵S△ABC=
| 1 |
| 2 |
∴ab=-8,
∵点C在双曲线上,
∴y=-
| 8 |
| x |
(3)∵CB⊥y轴,∴B(0,b),
在Rt△AOB中,AB=
| 17 |
根据勾股定理得:OB=4,
∴B(0,-4),
∴C(2,-4),
将C代入直线y=kx+k中,得:2k+k=-4,即k=-
| 4 |
| 3 |
∴直线AC解析式为y=-
| 4 |
| 3 |
| 4 |
| 3 |
联立直线与反比例解析式得:
|
解得:
|
|
∴D(-3,
| 8 |
| 3 |
则由图象可得:当x<-3或0<x<2时,反比例函数的值小于一次函数的值.

练习册系列答案
相关题目
 图象的两个交点.
图象的两个交点.



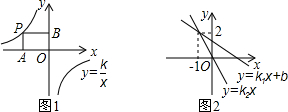 平面直角坐标系中的图象如图2所示,则关于x的不等式k1x+b>k2x的解为______.
平面直角坐标系中的图象如图2所示,则关于x的不等式k1x+b>k2x的解为______.