题目内容
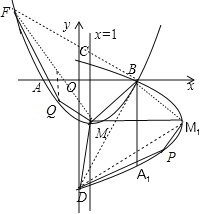
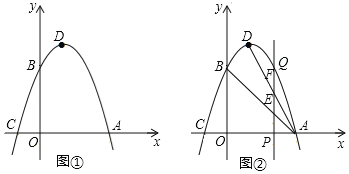
【题目】如图,抛物线y=![]() x2+bx+c的顶点为M,对称轴是直线x=1,与x轴的交点为A(-3,0)和B.将抛物线y=
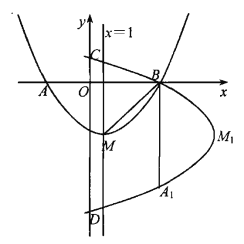
x2+bx+c的顶点为M,对称轴是直线x=1,与x轴的交点为A(-3,0)和B.将抛物线y=![]() x2+bx+c绕点B逆时针方向旋转90°,点M1,A1为点M,A旋转后的对应点,旋转后的抛物线与y轴相交于C,D两点.
x2+bx+c绕点B逆时针方向旋转90°,点M1,A1为点M,A旋转后的对应点,旋转后的抛物线与y轴相交于C,D两点.
(1)写出点B的坐标及求原抛物线的解析式:
(2)求证A,M,A1三点在同一直线上:
(3)设点P是旋转后抛物线上DM1之间的一动点,是否存在一点P,使四边形PM1MD的面积最大.如果存在,请求出点P的坐标及四边形PM1MD的面积;如果不存在,请说明理由.
【答案】(1)![]() (2)见试题解析;(3)∴点P的坐标为(
(2)见试题解析;(3)∴点P的坐标为(![]() ,-7)使四边形PM1MD的面积最大,面积最大值为
,-7)使四边形PM1MD的面积最大,面积最大值为![]()
【解析】
试题(1)根据抛物线的对称性即可写出B的坐标,根据对称轴是直线x=1,与x轴的交点为A(-3,0)代入即可得到方程组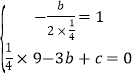 ,解方程组即可求出b、c的值,即可得到答案;
,解方程组即可求出b、c的值,即可得到答案;
(2)把x=1代入抛物线解析式即可得到M的坐标,根据旋转和图象即可求出M1、A1的坐标,设直线AM的表达式为y=kx+m,把A、M的坐标代入即可求出直线AM的解析式,根据以此函数图象上点的坐标特征确定点A1在直线AM上即可得到结论;
(3)连接M1D,如图,由于S△M1MD是定值,则要使四边形PM1MD的面积最大,只要S△M1PD最大,将△M1PD绕点B顺时针旋转90°,则点M1与点M重合,点P与点Q重合,点D与点F重合,利用旋转变换得点F的坐标为(-5,5),设点Q的坐标为(m,![]() ),易得直线MF的表达式为y=
),易得直线MF的表达式为y=![]() ,则根据三角形面积公式得到S△PDM1=S△QMF=
,则根据三角形面积公式得到S△PDM1=S△QMF=![]() (
(![]() -
-![]() )×(5+1)=
)×(5+1)=![]() ,根据二次函数的性质得当m=-2时,当m=-2时,S△M1PD最大=
,根据二次函数的性质得当m=-2时,当m=-2时,S△M1PD最大=![]() ,则点Q(-2,-
,则点Q(-2,-![]() ),利用旋转变换得点P的坐标为(
),利用旋转变换得点P的坐标为(![]() ,-7),然后计算S△DM1M的面积=24,再计算出四边形PM1MD的面积为24+
,-7),然后计算S△DM1M的面积=24,再计算出四边形PM1MD的面积为24+![]() =
=![]() .
.
试题(1)解:∵点B与点A(-3,0)关于直线x=1对称,
∴点B的坐标为(5,0),与x轴的交点为A(-3,0)代入即可得到方程组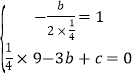 ,解得
,解得![]() ;
;
(2)点M1的坐标为(9,-4),点A1的坐标为(5,-8),设直线AM的表达式为y=kx+m,把A(-3,0),M(1,-4)代入解得,直线AM的解析式为y=-x-3,当x=5代入y=-x-3=-8,∴点A1在直线AM上,∴∠AMA1=180°;
(3)解:存在点P使四边形PM1MD的面积最大.
连接M1D,如图,∵S△M1MD是定值,∴要使四边形PM1MD的面积最大,只要S△M1PD最大,将△M1PD绕点B顺时针旋转90°,则点M1与点M重合,点P与点Q重合,点D与点F重合,则点Q,F都在抛物线y=![]() 上,由于F点的纵坐标为5,当y=5时,解得x1=-5,x2=7(舍去),∴点F的坐标为(-5,5),设点Q的坐标为(m,
上,由于F点的纵坐标为5,当y=5时,解得x1=-5,x2=7(舍去),∴点F的坐标为(-5,5),设点Q的坐标为(m,![]() )易得直线MF的表达式为y=
)易得直线MF的表达式为y=![]()
∴S△PDM1=S△QMF=![]() =
=![]()
当m=-2时,S△M1PD最大=![]() ∴点Q(-2,
∴点Q(-2,![]() ∴点P的坐标为(
∴点P的坐标为(![]() ,-7),
,-7),
∵点M的坐标为(1,-4),点M1的坐标为(9,-4),D(0,-10),
∴S△DM1M的面积=24,∴四边形PM1MD的面积为24+![]() =
=![]() ,∴点P的坐标为(
,∴点P的坐标为(![]() ,-7)使四边形PM1MD的面积最大,面积最大值为
,-7)使四边形PM1MD的面积最大,面积最大值为![]() .
.