Question

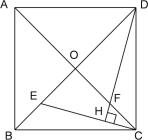
【题目】已知：如图，菱形ABCD的对角线AC与BD相交于点O，若∠CAD=∠DBC.

（1）求证：ABCD是正方形.

（2）E是OB上一点，DH⊥CE，垂足为H，DH与OC相交于点F，求证：OE=OF.

Answer 1

【答案】（1）见解析；（2）见解析.

【解析】

（1）利用菱形的对角线平方每组对角即可求解证明；（2）根据已知条件证得△ECO≌△FDO，即可得证.

（1）证明：∵四边形是菱形，

∴，∠BAD=2∠DAC, ∠ABC=2∠DBC ;

∴∠DAB+∠ABC=180°;

∵∠DAC=∠DBC;

∴∠BAD=∠ABC,

∴2∠BAD=180°;

∴∠BAD=90°;

∴四边形ABCD是正方形.

（2）证明：∵四边形ABCD是正方形；

∴AC⊥BD,AC=BD,CO=AC，DO=BO

∴∠COB=∠DOC=90°，CO=DO

∵DH⊥CE，垂足为H；

∴∠DHE=90°，∠EDH+∠DEH=90°

又∵∠ECO+∠DEH=90°

∴∠ECO=∠EDH

∴△ECO≌△FDO；

∴.