题目内容
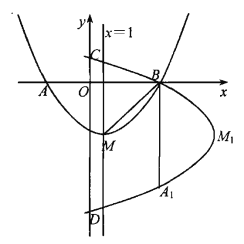
【题目】已知二次函数y=ax2+bx+3的图象分别与x轴交于点A(3,0),C(-1,0),与y轴交于点B.点D为二次函数图象的顶点.
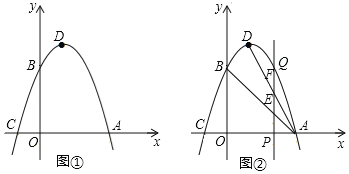
(1)如图①所示,求此二次函数的关系式:
(2)如图②所示,在x轴上取一动点P(m,0),且1<m<3,过点P作x轴的垂线分别交二次函数图象、线段AD,AB于点Q、F,E,求证:EF=EP;
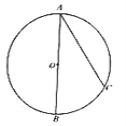
(3)在图①中,若R为y轴上的一个动点,连接AR,则![]() BR+AR的最小值______(直接写出结果).
BR+AR的最小值______(直接写出结果).
【答案】(1)y=-x2+2x+3;(2)见解析;(3)![]()
【解析】
(1)根据A,C点的坐标,利用待定系数法可求出二次函数的关系式;
(2)利用待定系数法求出线段AB,AD所在直线的函数关系式,用m表示EF,EP的长,可证得结论;
(3)连接BC,过点R作RQ⊥BC,垂足为Q,则△BQR∽△AOB,利用相似三角形的性质可得出RQ=![]() BR,结合点到直线之间垂直线段最短可得出当A,R,Q共线且垂直AB时,即AR+
BR,结合点到直线之间垂直线段最短可得出当A,R,Q共线且垂直AB时,即AR+![]() BR=AQ时,其值最小,由∠ACQ=∠BCO,∠BOC=∠AQC可得出△CQA∽△COB,利用相似三角形的性质可求出AQ的值,此题得解.
BR=AQ时,其值最小,由∠ACQ=∠BCO,∠BOC=∠AQC可得出△CQA∽△COB,利用相似三角形的性质可求出AQ的值,此题得解.
解:(1)将A(3,0),C(-1,0)代入y=ax2+bx+3,得:
![]() ,解得:
,解得:![]() ,
,
∴此二次函数的关系式为y=-x2+2x+3.
(2)证明:∵y=-x2+2x+3=-(x-1)2+4,
∴点D的坐标为(1,4).
设线段AB所在直线的函数关系式为y=kx+c(k≠0),
将A(3,0),C(0,3)代入y=kx+c,得:
![]() ,解得:
,解得:![]() ,
,
∴线段AB所在直线的函数关系式为y=-x+3.
同理,可得出:线段AD所在直线的函数关系式为y=-2x+6.
∵点P的坐标为(m,0),
∴点E的坐标为(m,-m+3),点F的坐标为(m,-2m+6),
∴EP=-m+3,EF=-m+3,
∴EF=EP.
(3)如图③,连接BC,过点R作RQ⊥BC,垂足为Q.
∵OC=1,OB=3,
∴BC=![]() .(勾股定理)
.(勾股定理)
∵∠CBO=∠CBO,∠BOC=∠BQR=90°,
∴△BQR∽△AOB,
∴![]() ,即
,即![]() ,
,
∴RQ=![]() BR,
BR,
∴AR+![]() BR=AR+RQ,
BR=AR+RQ,
∴当A,R,Q共线且垂直AB时,即AR+![]() BR=AQ时,其值最小.
BR=AQ时,其值最小.
∵∠ACQ=∠BCO,∠BOC=∠AQC,
∴△CQA∽△COB,
∴![]() ,即
,即![]()
∴AQ=![]() ,
,
∴![]() BR+CR的最小值为
BR+CR的最小值为![]() .
.
故答案为:![]() .
.

【题目】某校初一年级68名师生参加社会实践活动,计划租车前往,租车收费标准如下:
车型 | 大巴车 (最多可坐55人) | 中巴车 (最多可坐39人) | 小巴车 (最多可坐26人) |
每车租金 (元∕天) | 900 | 800 | 550 |
则租车一天的最低费用为____元.