Question

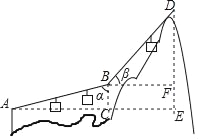
【题目】如图，游客在点A处坐缆车出发，沿A﹣B﹣D的路线可至山顶D处．已知AB＝BD＝800米，∠α＝75°，∠β＝45°，求山高DE（结果精确到1米）．（参考数据：sin75°＝0.966，cos75°＝0.259，tan75°＝3.732，＝1.414）

Answer 1

【答案】山高DE约为773米．

【解析】

在R△ABC中，求出BC＝ABcos75°≈800×0.26＝208m，在Rt△BDF中，求出DF的长，由四边形BCEF是矩形，可得EF＝BC，由此即可解决问题．

解：由题意得：∠ACB＝∠BFD＝90°，EF＝BC，

在Rt△ABC中，∠ACB＝90°，cosα＝，

∴BC＝ABcos75°＝80×0.259＝207.2．

∴EF＝BC＝207.2，

在Rt△BDF中，∠BFD＝90°，sinβ＝，

∴DF＝BDsin45°＝800×＝400×1.414＝565.6．

∴DE＝DF+EF＝565.6+207.2＝772.8≈773（米）．

∴山高DE约为773米．