题目内容
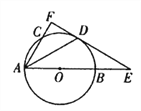
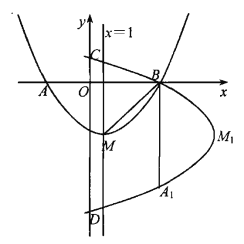
【题目】如图,抛物线y=ax2+bx+4与x轴交于A,B两点,与y轴交于点C,已知点A(-2,0),B(8,0),连接AC,BC.
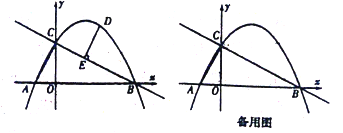
(1)求抛物线的解析式和点C的坐标;
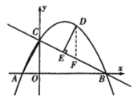
(2)点D是直线BC上方抛物线上的一点,过点D作DE⊥BC,垂足为E,求线段DE的长度最大时,点D的坐标;
(3)抛物线上是否存在一点P(异于点A,B,C),使![]() ?若存在,请直接写出点P的坐标;若不存在,请说明理由.
?若存在,请直接写出点P的坐标;若不存在,请说明理由.
【答案】(1)抛物线的解析式为![]() ,点
,点![]() 的坐标为
的坐标为![]() ;(2)点
;(2)点![]() 的坐标为
的坐标为![]() ;(3)存在点
;(3)存在点![]() ,使
,使![]() ,点
,点![]() 的坐标为
的坐标为![]() 或
或![]()
【解析】
(1)把A、B两点的坐标代入,解方程组即可得到抛物线的解析式,令x=0求出y的值,即可得到C的坐标;
(2)如图,过点D作DF//y轴,交BC于F点,则∠DFE=∠BCO,由勾股定理,得到BC的长,由正弦的定义得到DE=DFsin∠DFE=DFsin∠BCO=![]() DF.
DF.
求出直线BC的解析式.设![]() ,则
,则![]() ,得到DF
,得到DF![]() ,由DE=
,由DE=![]() DF,配方即可得出结论;
DF,配方即可得出结论;
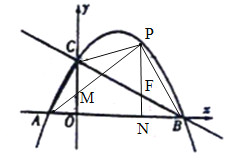
(3)如图,连接PC,PB,PA交OC于M,作PN⊥x轴于N交CB于F.设P(m,![]() ),则F(m,
),则F(m,![]() ),分两种情况讨论:①若P在x轴上方,表示出PF的长,得到
),分两种情况讨论:①若P在x轴上方,表示出PF的长,得到![]() =
=![]() .由相似三角形的判定与性质得到AO:AN=OM:PN,进而得出OM,CM的长,得到
.由相似三角形的判定与性质得到AO:AN=OM:PN,进而得出OM,CM的长,得到![]() =
=![]() .由
.由![]() ,解方程即可得出点P的坐标.
,解方程即可得出点P的坐标.
②当P在x轴下方时,类似可得点P的坐标.
(1)把A(-2,0),B(8,0)分别代入y=ax2+bx+4中,得:![]() ,解得:
,解得: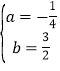 ,∴抛物线的解析式为
,∴抛物线的解析式为![]() ;
;
令x=0,得y=4,∴点C的坐标为(0,4).
(2)如图,过点D作DF//y轴,交BC于F点,则∠DFE=∠BCO,C(0,4),B(8,0),∴OC=4,OB=8.
在RtΔOBC中,由勾股定理,得:BC=![]()
![]() ,∴sin∠BCO=
,∴sin∠BCO=![]() ,∴在RtΔDEF中,DE=DFsin∠DFE=DFsin∠BCO=
,∴在RtΔDEF中,DE=DFsin∠DFE=DFsin∠BCO=![]() DF.
DF.
设直线BC的解析式为y=kx+t,把B(8,0),C(0,4)分别代入,得:![]() ,解得:
,解得: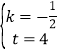 ,∴直线BC的解析式为
,∴直线BC的解析式为![]() ;
;
设![]() ,则
,则![]() ,∴DF=
,∴DF=![]() ,∴DE=
,∴DE=![]() DF
DF![]()
∵![]() ,∴当m=4时,DE的值最大,最大值为
,∴当m=4时,DE的值最大,最大值为![]() ,此时点D的坐标为(4,6).
,此时点D的坐标为(4,6).
(3)如图,连接PC,PB,PA交OC于M,作PN⊥x轴于N交CB于F.设P(m,![]() ),则F(m,
),则F(m,![]() ),分两种情况讨论:①若P在x轴上方,∴PF=
),分两种情况讨论:①若P在x轴上方,∴PF=![]() ,
,![]() =
=![]() =
=![]() .
.
∵AO=2,ON=m,∴AN=m+2.
∵MO∥PN,∴△AOM∽△ANP,∴AO:AN=OM:PN,∴2:(m+2)=OM:![]() ,∴OM=
,∴OM=![]() ,∴CM=CO-OM=
,∴CM=CO-OM=![]() =
=![]() ,∴
,∴![]() =
=![]() =
=![]() .
.
∵![]() ,∴
,∴![]() .
.
∵m≠0,∴m=6.当m=6时,![]() =4,∴点P的坐标为(6,4).
=4,∴点P的坐标为(6,4).
②当P在x轴下方时,类似可得:![]() .
.
∵m≠0,∴m=![]() .当m=
.当m=![]() 时,
时,![]() =
=![]() ;∴点P的坐标为
;∴点P的坐标为![]() .
.
综上所述:存在点P,使![]() ,点P的坐标为(6,4)或
,点P的坐标为(6,4)或![]() .
.