题目内容
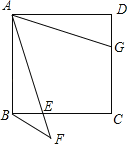
【题目】如图，等边
边长为
，点
是的内心，
，绕点旋转
，分别交线段
、
于
、
两点，连接
，给出下列四个结论：①
形状不变；②的面积最小不会小于四边形
的面积的四分之一；③四边形的面积始终不变；④
周长的最小值为
．上述结论中正确的个数是（ ）
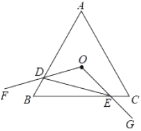
A.4B.3C.2D.1
【答案】A
【解析】
连接OB、OC，利用SAS证出△ODB≌△OEC，从而得出△ODE是顶角为120°的等腰三角形，即可判断①；过点O作OH⊥DE，则DH=EH，利用锐角三角函数可得OH=
OE和DE=
OE，然后三角形的面积公式可得S△ODE=
OE2，从而得出OE最小时，S△ODE最小，根据垂线段最短即可求出S△ODE的最小值，然后证出S四边形ODBE=S△OBC=
即可判断②和③；求出
的周长=a＋DE，求出DE的最小值即可判断④．
解：连接OB、OC
∵
是等边三角形，点
是的内心，
∴∠ABC=∠ACB=60°，BO=CO，BO、CO平分∠ABC和∠ACB
∴∠OBA=∠OBC=∠ABC=30°，∠OCA=∠OCB=∠ACB=30°
∴∠OBA=∠OCB，∠BOC=180°－∠OBC－∠OCB=120°
∵
∴
∠BOC
∴∠FOG－∠BOE=∠BOC－∠BOE
∴∠BOD=∠COE
在△ODB和△OEC中
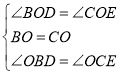
∴△ODB≌△OEC
∴OD=OE
∴△ODE是顶角为120°的等腰三角形，
∴
形状不变，故①正确；
过点O作OH⊥DE，则DH=EH
∵△ODE是顶角为120°的等腰三角形
∴∠ODE=∠OED=（180°－120°）=30°
∴OH=OE·sin∠OED=OE，EH= OE·cos∠OED=
OE
∴DE=2EH=OE
∴S△ODE=DE·OH=OE2
∴OE最小时，S△ODE最小，
过点O作OE′⊥BC于E′，根据垂线段最短，OE′即为OE的最小值
∴BE′=BC=
在Rt△OBE′中
OE′=BE′·tan∠OBE′=×
=
∴S△ODE的最小值为OE′2=
∵△ODB≌△OEC
∴S四边形ODBE=S△ODB＋S△OBE= S△OEC＋S△OBE=S△OBC=BC·OE′=
∵=
×
∴S△ODE≤S四边形ODBE
即的面积最小不会小于四边形
的面积的四分之一，故②正确；
∵S四边形ODBE=
∴四边形的面积始终不变，故③正确；
∵△ODB≌△OEC
∴DB=EC
∴的周长=DB＋BE＋DE= EC＋BE＋DE=BC＋DE=a＋DE
∴DE最小时的周长最小
∵DE=OE
∴OE最小时，DE最小
而OE的最小值为OE′=
∴DE的最小值为×=
∴的周长的最小值为a＋=
，故④正确；
综上：4个结论都正确，
故选A．
