题目内容
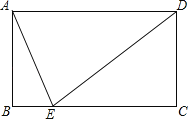
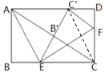
【题目】如图,在矩形![]() 中,
中,![]() ,点
,点![]() ,
,![]() 分别在
分别在![]() ,
,![]() 上,将
上,将![]() 沿
沿![]() 折叠,使点
折叠,使点![]() 落在
落在![]() 上的点
上的点![]() 处,又将
处,又将![]() 沿
沿![]() 折叠,使点
折叠,使点![]() 落在直线
落在直线![]() 与
与![]() 的交点
的交点![]() 处.
处.
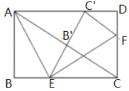
(1)求证:点![]() 在
在![]() 的角平分线上;
的角平分线上;
(2)求![]() 的长.
的长.
【答案】(1)见解析;(2)![]()
【解析】
(1)连接CC′根据矩形的性质和平行线的性质可得∠DC′C=∠ECC′,由折叠的性质,∠ECC′=∠EC′C,从而得出∠EC′C=∠DC′C,最后根据角平分线的定义即可证出结论;
(2)由折叠的性质可得AB=AB′,∠B=∠AB′E=90°,C′F=CF,∠EC′F=∠ECF=90°,然后证出∠DAC=30°,结合矩形的性质、四边形的内角和求出∠DC′F=30°,从而得出C′F=2DF,最后根据CF+DF=CD即可求出结论.
(1)证明:连接CC′
∵四边形ABCD为矩形
∴AD∥BC
∴∠DC′C=∠ECC′
由折叠的性质,∠ECC′=∠EC′C
∴∠EC′C=∠DC′C
∴点![]() 在
在![]() 的角平分线上;
的角平分线上;
(2)由折叠的性质可得AB=AB′,∠B=∠AB′E=90°,C′F=CF,∠EC′F=∠ECF=90°
∴CB′⊥C′B′,
∵C′C平分∠B′C′D,∠D=90°,CD=AB=a
∴CD=CB′
∴CD=AB′= CB′
∴AC=2CD
∴∠DAC=30°,
∴∠ACD=90°-∠DAC=60°
∴∠B′C′D=360°-∠C′B′C-∠D-∠ACD=120°
∴∠DC′F=∠B′C′D-∠EC′F=30°
在Rt△DC′F中,C′F=2DF
∴CF=2DF
∵CF+DF=CD=a
∴3DF=a
∴DF=![]()

【题目】目前“微信”以其颠覆性的创新,赢得了数亿人的支持,为了调查某中学学生在周日上“微信”的时间,随机对100名男生和100名女生进行了问卷调查,得到了如下的统计结果
表1:男生上“微信时间的频数分布表
上网时间(分钟) | 30≤x<40 | 40≤x<50 | 50≤x<60 | 60≤x<70 | 70≤x<80 |
人数 | 5 | 25 | 30 | 25 | 15 |
表2:女生上“微信”时间的频数分布表
上网时间(分钟) | 30≤x<40 | 40≤x<50 | 50≤x<60 | 60≤x<70 | 70≤x<80 |
人数 | 10 | 20 | 40 | 20 | 10 |
请结合图表完成下列各题
(1)完成表3:
表3 | 上“微信”时间少于60分钟 | 上“微信”时间不少于60分钟 |
男生人数 |
|
|
女生人数 |
|
|
(2)若该中学共有女生750人,请估计其中上“微信”时间不少于60分钟的人数;
(3)从表3的男生中抽取5人(其中3人上“微信”时间少于60分钟,2人上“微信”时间不少于60分钟),再从抽取的5人中任取2人,请用列表或画树状图的方法求出至少有一人上“微信”时间不少于60分钟的概率.