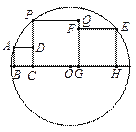Question

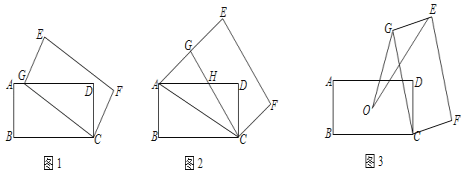
【题目】已知，如图1，为正方形边的中点，，连接，．

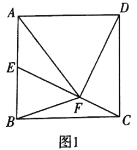
（1）求证：①；

②；

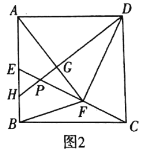
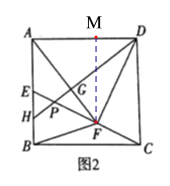
（2）如图2，若，作，分别交，于点，，求的长．

Answer 1

【答案】（1）①见详解，②见详解；（2）2

【解析】

（1）①由为正方形边的中点，得BE=，易证DFC~CBE，得，进而即可得到结论；②过点F作FM⊥AD，垂足为点M，CF=a，则DF=2a，DC=，用含a得代数式表示出AF的长，进而得到AF= AB，即可得到结论；

（2）过点F作FM⊥AD，垂足为点M，由第（1）②小题，可知：a=，得到DG=MF=，由余弦函数的定义得，从而得到DH，AH，EH的长，结合，即可求解．

（1）①∵为正方形边的中点，

∴BE=，

∵在正方形ABCD中，，

∴∠CDF+∠DCF=90°，∠DCF+∠ECB=90°，

∴∠CDF=∠ECB，

又∵∠DFC=∠CBE=90°，

∴DFC~CBE，

∴=，即：；

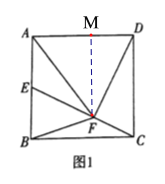
②过点F作FM⊥AD，垂足为点M，

∴FM∥CD，

∴∠MFD=∠CDF，

∴在Rt MFD与Rt CDF中，tan∠MFD=tan∠CDF==，

设CF=a，则DF=2a，DC=，

∵tan∠MFD==，DF2=MD2+MF2，

∴MD：MF：DF=1：2：，

∴MD==，MF=2MD=，

∵AD= DC=，

∴AM= AD- MD=，

∴AF==，

∵AB=CD=，

∴AF= AB，

∴；

（2）过点F作FM⊥AD，垂足为点M，

由（1）②小题可知：，即：a=，

∴MF==，AD=AB=CD=8，

∵AB=AF=AD，，FM⊥AD，

∴DG=MF=，

∵cos∠ADH=，

∴DH===10，

∴AH=，

∵AE=AB=4，

∴EH=6-4=2，

∵AB∥CD，

∴，即：，

∴HP=2．