Question

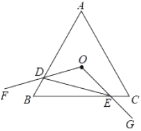
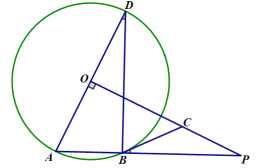
【题目】如图，在△ABC中，AB＝AC，⊙O分别切AB于M，BC于N，连接BO、CO，BO＝CO．

（1）求证：AC是⊙O的切线；

（2）连接MC，若，求sin∠B的值．

Answer 1

【答案】（1）见解析；（2）．

【解析】

（1）连接NO，过点O作OE⊥AC于点E，由 可得∠ABC=∠ACB，结合，证明利用角平分线的性质可得NO=EO，则结论得证；

（2）过点M作MF⊥BC于点F，连结OM，ON，证得BM=BN=BC，设BC=a，CF=b，则MF=b，BF=a-b，BM=a，可得，解方程得b=，可求出答案．

（1）证明：如图1，连接NO，过点O作OE⊥AC于点E，

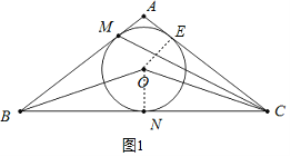
∵AB＝AC，

∴∠ABC＝∠ACB，

∵⊙O分别切AB于M，BC于N，

∠ABO＝∠CBO，

∴

∵ON⊥BC，OE⊥AC，

∴NO＝EO，

∴AC是⊙O的切线；

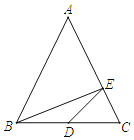
（2）解：如图2，过点M作MF⊥BC于点F，连结OM，ON，

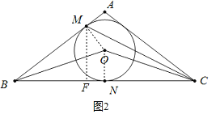
∵OM＝ON，OB＝OB，

∴Rt△BOM≌Rt△BON（HL），

∴BM＝BN，

∵OB＝OC，ON⊥BC，

∴BN＝CN＝BC，

∴

∵

∴，

∴，

设BC＝a，CF＝b，则MF＝，BF＝a﹣b，BM＝，

∵

∴，

解得b＝或b＝a（舍去）．

∴