题目内容
【题目】如图,在矩形ABCD中,已知AB=8cm,BC=10cm,折叠矩形的一边AD , 使点D落在BC边的中点F处,折痕为AE , 求CE的长.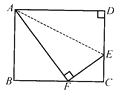
【答案】解答:解:根据题意可得:BC=AD=AF=10cm,DE=DF ,
∵在ABF中,∠ABF=90°,
∴ ![]() cm,
cm,
∴FC=BC-BF=4cm,设CE=x , 那么EF=DE=8-x ,
又∵∠C=90°,所以 ![]() 即
即 ![]() ,
,
∴x=3,
∴CE=3cm.
【解析】通过翻折的性质,将所求和已知的线段转换到同一个三角形中是解题的关键.
【考点精析】解答此题的关键在于理解勾股定理的概念的相关知识,掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2,以及对矩形的性质的理解,了解矩形的四个角都是直角,矩形的对角线相等.

练习册系列答案
相关题目
【题目】在我市实施“城乡环境综合治理”期间,某校组织学生开展“走出校门,服务社会”的公益活动.八年级一班王浩根据本班同学参加这次活动的情况,制作了如下的统计图表:
该班学生参加各项服务的频数、频率统计表:
服务类别 | 频数 | 频率 |
文明宣传员 | 4 | 0.08 |
文明劝导员 | 10 | |
义务小警卫 | 8 | 0.16 |
环境小卫士 | 0.32 | |
小小活雷锋 | 12 | 0.24 |
请根据上面的统计图表,解答下列问题:
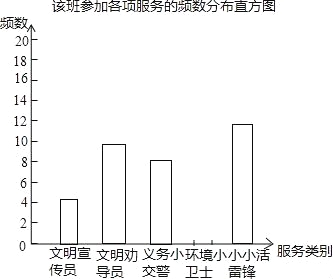
(1)该班参加这次公益活动的学生共有 名;
(2)请补全频数、频率统计表和频数分布直方图;
(3)若八年级共有900名学生报名参加了这次公益活动,试估计参加文明劝导的学生人数.