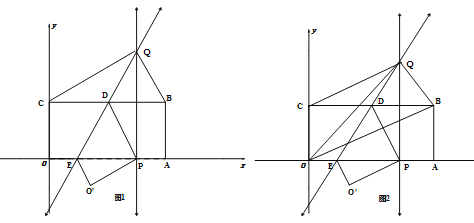��Ŀ����
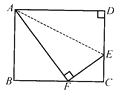
����Ŀ����ͼ��ʾ����ƽ��ֱ������ϵ�У�����ABCD�ı�AD��x���ϣ���A��ԭ�㣬AB=3��AD=6����������ÿ��2����λ������x���������������˶���ͬʱ��P��A�������ÿ��1����λ������A��B��C��D��·���������˶�����P���˶���D��ʱֹͣ�˶�������ABCDҲ��ֹ֮ͣ�˶���
��1����P���A���˶���D�������ʱ�䣻
��2����P����˶�ʱ��Ϊt���룩��
�ٵ�t=8ʱ�������P�����ꣻ
������OAP���ΪS����̽����P���˶�������S��t֮��Ĺ�ϵʽ��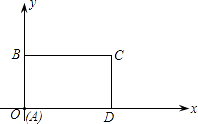
���𰸡�
��1��
�⣺P���A���˶���D�������ʱ��=��3+6+3����1=12���룩
��2��
�⣺�ٵ�t=8ʱ��P���A���˶�����BC�ϣ�
��ͼ��

����P��PE��AD�ڵ�E��
��ʱA�㵽E���ʱ��=8�룬AB+BP=8��
��BP=5����PE=AB=3��AE=BP=5
�߾��������ƶ�2��8=16
��OE=OA+AE=16+5=21
���P��������21��3����
�ڷ����������
��0��t��3ʱ����P��AB���˶�����ʱOA=2t��AP=t
��s= ![]() ��2t��t=t2
��2t��t=t2
��3��t��9ʱ����P��BC���˶�����ʱOA=2t
��s= ![]() ��2t��3=3t
��2t��3=3t
��9��t��12ʱ����P��CD���˶�����ʱOA=2t��AB+BC+CP=t
��DP=��AB+BC+CD������AB+BC+CP��=12��t
��s= ![]() ��2t����12��t��=��t2+12t����������s��t֮��ĺ�����ϵʽ�ǣ�s=
��2t����12��t��=��t2+12t����������s��t֮��ĺ�����ϵʽ�ǣ�s= 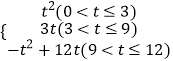
����������1�����AB+BC+CD���ɵó����ۣ���2�������жϳ���P�ڱ�BC�ϣ������ƶ��ĵ�λ������ȷ������������ƽ�Ƶĵ�λ�����ɵó����ۣ��ڷ�����������������ε������ʽ������⣮
�����㾫�������ڱ��⿼���ƽ���ı��ε��ж������ʣ���Ҫ�˽���һֱ�߹�ƽ���ı������Խ��ߵĽ��㣬������ֱ�߱�һ��Ա߽��µ��߶��ԶԽ��ߵĽ���Ϊ�е㣬����������ֱ�߶��ȷִ�ƽ���ı��ε�������ܵó���ȷ�𰸣�

 ��ѧȫ��������ѵ��ϵ�д�
��ѧȫ��������ѵ��ϵ�д�����Ŀ�����ؿ�����ij���ӵ�·�峧������ɽ��ѧ��2014��Ӧ���ҵ������Ƹ��˾ְԱ����ӦƸ�ߵ�רҵ֪ʶ��Ӣ��ˮƽ���μ����ʵ�������Ż��������в��Ի�ɹ��϶�������ĵ÷����ֶ�Ϊ100�֣�����ķ����ֱ�5��3��2�ı�������ÿ�˵�����ܷ֣���4λӦƸ�ߵĵ÷������
�÷� | רҵ֪ʶ | Ӣ��ˮƽ | �μ����ʵ���� |
�� | 85 | 85 | 90 |
�� | 85 | 85 | 70 |
�� | 80 | 90 | 70 |
�� | 90 | 90 | 50 |
��1���ֱ����4λӦƸ�ߵ��ܷ֣�
��2���������ˡ�רҵ֪ʶ����ƽ����Ϊ85�֣�����Ϊ12.5�����ˡ�Ӣ��ˮƽ����ƽ����Ϊ87.5�֣�����Ϊ6.25������������ˡ��μ����ʵ�������Ż�ȡ���ƽ���ּ����
��3��������1���ͣ�2���е��й����ݣ���Դ�ѧ��ӦƸ���кν��飿