Question

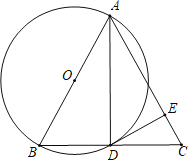
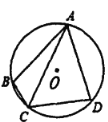
【题目】如图，在圆内接四边形中，，，，则四边形的面积为（ ）

A.1B.C.D.

Answer 1

【答案】D

【解析】

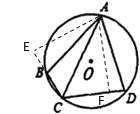
过点A作AE⊥BC于E，AF⊥CD于F，则∠E=∠AFC=,由AAS可证△ABE≌△ADF，得出AE=AF，再根据HL可证Rt△AEC≌Rt△AFC，得到四边形的面积=2S△AFC，求出△AFC的面积即可.

过点A作AE⊥BC于E，AF⊥CD于F，则∠E=∠AFC=,

∵四边形ABCD是圆内接四边形，

∴∠D+∠ABC=，

∵∠ABE+∠ABC=,

∴∠D=∠ABE,

又∵，

∴△ABE≌△ADF,

∴四边形的面积=四边形AECF的面积,AE=AF,

∵∠E=∠AFC,AC=AC,

∴Rt△AEC≌Rt△AFC,

∵,∠AFC=,

∴∠CAF=,

∴CF==，

∴AF=，

∴四边形的面积=2S△AFC= .