Question

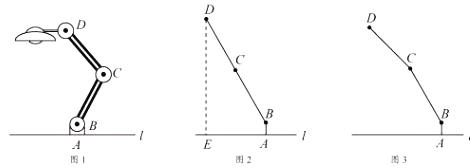
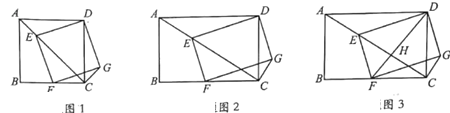
【题目】在矩形ABCD中，AB=a，AD=b，点E为对角线AC上一点，连接DE，以DE为边，作矩形DEFG，点F在边BC上；

（1）观察猜想：如图1，当a=b时，=______，∠ACG=______；

（2）类比探究：如图2，当a≠b时，求的值（用含a、b的式子表示）及∠ACG的度数；

（3）拓展应用：如图3，当a=6，b=8，且DF⊥AC，垂足为H，求CG的长；

Answer 1

【答案】（1）1，90°；（2）∠ACG =90°，；（3）CG=.

【解析】

（1）利用SAS可证，由全等三角形的性质知，所以，结合可得；

（2）方法一：过点E作EM⊥BC,EN⊥DC,垂足分别为M和N，连接EG,FD交于点O,连接OC，利用矩形的性质及三角形内角和定理可得∠ACG =90°，可证△DAE∽△DCG，由相似三角形的对应线段成比例可得的值；方法二：结合垂直与矩形的性质由两组对应角分别相等的两个三角形相似可得△CEN∽△CAD，△END∽△EMF，由相似三角形的性质可得，，由两组对应线段成比例及其夹角相等的两个三角形相似可得△ADE∽△CDG，根据其性质可得结论；

（3）由勾股定理得AC长，由相似三角形的判定可得△ CDH∽△CAD，△DEF∽△ADC，由相似三角形的性质可得CH的长及∠EDH=∠CAD，利用AAS得 △DHE≌△DHC，根据全等的性质可得EH的长，进一步可知AE长，结合即知CG的值.

解：（1）根据题意，易知矩形ABCD与矩形DEFG为正方形

（2）方法一：连接EG,FD交于点O,连接OC.

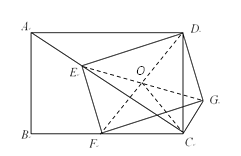
∵四边形EDGF和ABCD是矩形

∴∠ADC=∠EDG=90°

即∠ADE+∠EDC=∠CDG+∠EDC

∴∠ADE =∠CDG

∵∠ BCD=90°OF=OD

∴OC=

在矩形DEFG中，EG=DF ∴ OC=

∵OE=OG ∴OE=OC=OG

∴∠OEC=∠OCE ∠OCF=∠OFC

又∵∠OEC+∠ECG+∠EGC=180°

∴2∠OCE+2∠OCG =180°

∴∠OCE+∠OCG =90°即∠ACG =90°

∴∠ECD+∠DCG =90°

在Rt△ADC中，∠ECD+∠DAC =90°∴∠DAE=∠DCG

∴△DAE∽△DCG

∴

方法二：过点E作EM⊥BC,EN⊥DC,垂足分别为M和N.

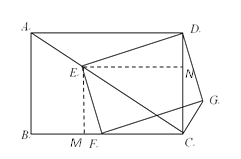
∵∠EMC=∠MCN=∠ENC=90°

∴四边形EMCN是矩形

∴EM=NC,∠MEN=90°.

∵∠ ENC =∠ADC=90°∴EN∥AD

∴△CEN∽△CAD

∴即

∵∠MEN=90°∠FED=90°

∴∠MEF=∠NED

又∵∠END =∠EMF =90°

∴△END∽△EMF

∴

又∵EF=DG∴

∵∠ADC=∠EDG=90°

∴△ADE∽△CDG

∴ , ∠DAE=∠DCG

∵在Rt△ADC中∠DAC+∠ACD=90°

∴∠ACG=∠DCG+∠ACD=90°

(3) ∵AD=8,DC=6 ∴AC==10

∵DF⊥AC∴，∠CDH +∠ACD=90°

∵∠DAC+∠ACD=90°

∴∠CDH=∠DAC

∴△ CDH∽△CAD

∴CD2=CH·CA ,∠CDH=∠CAD

∵CD=6,AC=10

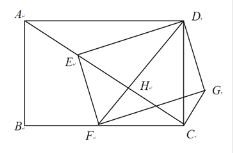
∴CH=

∵ 由（2）知 ∠DEF =∠ADC =90°

∴△DEF∽△ADC

∴∠EDH=∠CAD

∴∠CDH=∠EDH

∵∠DHE=∠DHC=90°DH=DH

∴△DHE≌△DHC

∴EH=CH=

∴AE=AC-EH-HC=

∵∴CG=