题目内容
【题目】我们规定抛物线![]() 与
与![]() 轴有两个不同的交点
轴有两个不同的交点![]() ,
,![]() 时,线段
时,线段![]() 称为该抛物线的“横截弦”,其长度记为
称为该抛物线的“横截弦”,其长度记为![]() .
.
(1)已知抛物线![]() ,则
,则![]() ;
;
(2)已知抛物线![]() 经过点
经过点![]() ,当
,当![]() 时,求该抛物线所对应的函数解析式;
时,求该抛物线所对应的函数解析式;
(3)已知抛物线![]() 经过点
经过点![]() ,与
,与![]() 轴交于点
轴交于点![]() .
.
①抛物线恒存在“横截弦”,求![]() 的取值范围;
的取值范围;
②求![]() 关于
关于![]() 的函数解析式;
的函数解析式;
③连接![]() ,
,![]() ,
,![]() 的面积为
的面积为![]() .当
.当![]() 时,请直接写出
时,请直接写出![]() 取值范围.
取值范围.
【答案】(1)![]() ;(2)
;(2)![]() 或y=
或y=![]() ;(3)①
;(3)①![]() ;②当
;②当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() ;③
;③![]() 或
或![]() ;
;
【解析】
(1)令y=0,得2x2-x-3=0,解得,x1=-1,![]() ,得d=|x1-x2|=
,得d=|x1-x2|=![]() ;
;
(2)经过点A(1,0),d=2,则抛物线与x轴另一个交点是(-1,0)或(3,0),分别代入解析式即可求y=-2x2+2或y=![]() ;
;
(3)将A(1,0)代入y=-x2+bx+c得b+c=1;①抛物线恒存在“横截弦”,△=(1-c)2+4c=c2+2c+1>0;②![]() ,当c>-1时,d=c+1,当c<-1时,d=-c-1;③
,当c>-1时,d=c+1,当c<-1时,d=-c-1;③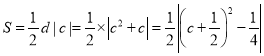 ,1≤S≤10,-5≤c≤-2或1≤c≤4;
,1≤S≤10,-5≤c≤-2或1≤c≤4;
解:(1)令![]() ,得
,得![]() ,
,
解得,![]() ,
,![]() ,
,
![]() ,
,
故答案为:![]() ;
;
(2)经过点![]() ,
,![]() ,
,
∴抛物线与![]() 轴另一个交点是
轴另一个交点是![]() 或
或![]() ,
,
将![]() 代入
代入![]() ,得
,得![]() ,
,
将![]() 代入
代入![]() ,得
,得![]() ,
,
将![]() 代入
代入![]() ,得
,得![]() ,
,
![]() ,
,![]() 或
或![]() ,
,![]() ,
,
![]() 或
或![]() ;
;
(3)将![]() 代入
代入![]() 得
得![]() ;
;
![]() ,
,
令![]() ,得
,得![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
①抛物线恒存在“横截弦”,
![]() ,
,
![]() ;
;
②![]() ,
,
当![]() 时,
时,![]() ,
,
当![]() 时,
时,![]() ;
;
③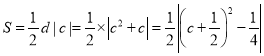 ,
,
![]() ,
,
![]() 或
或![]() ;
;

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目