题目内容
【题目】某商店老板准备购买A、B两种型号的足球共100只,已知A型号足球进价每只40元,B型号足球进价每只60元.
(1)若该店老板共花费了5200元,那么A、B型号足球各进了多少只;
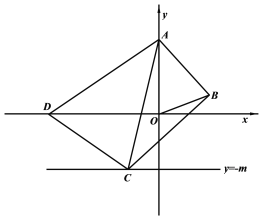
(2)若B型号足球数量不少于A型号足球数量的![]() ,那么进多少只A型号足球,可以让该老板所用的进货款最少?
,那么进多少只A型号足球,可以让该老板所用的进货款最少?
【答案】(1)A型足球进了40个,B型足球进了60个;(2)当x=60时,y最小=4800元.
【解析】
(1)设A型足球x个,则B型足球(100-x)个,根据该店老板共花费了5200元列方程求解即可;
(2)设进货款为y元,根据题意列出函数关系式,根据B型号足球数量不少于A型号足球数量的![]() 求出x的取值范围,然后根据一次函数的性质求解即可.
求出x的取值范围,然后根据一次函数的性质求解即可.
解:(1)设A型足球x个,则B型足球(100-x)个,
∴ 40x +60(100-x)=5200 ,
解得:x=40 ,
∴100-x=100-40=60个,
答:A型足球进了40个,B型足球进了60个。
(2)设A型足球x个,则B型足球(100-x)个,
100-x≥![]() ,
,
解得:x≤60 ,
设进货款为y元,则y=40x+60(100-x)=-20x+6000 ,
∵k=-20,∴y随x的增大而减小,
∴当x=60时,y最小=4800元.

练习册系列答案
相关题目