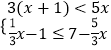题目内容
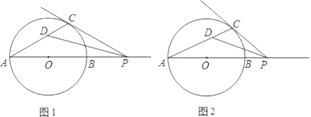
【题目】已知AB为⊙O的直径,P为AB延长线上的任意一点,过点P作⊙O的切线,切点为C,∠APC的平分线PD与AC交于点D.
(1)如图1,若∠CPA恰好等于30°,求∠CDP的度数;
(2)如图2,若点P位于(1)中不同的位置,(1)的结论是否仍然成立?说明你的理由.
【答案】(1)∠CDP=45°;
(2)∠CDP的大小不发生变化,理由见解析.
【解析】试题分析:(1)连接OC,则∠OCP=90°,根据∠CPA=30°,求得∠COP,再由OA=OC,得出∠A=∠ACO,由PD平分∠APC,即可得出∠CDP=45°.(2)由PC是⊙O的切线,得∠OCP=90°.再根据PD是∠CPA的平分线,得∠APC=2∠APD.根据OA=OC,可得出∠A=∠ACO,即∠COP=2∠A,在Rt△OCP中,∠OCP=90°,则∠COP+∠OPC=90°,从而得出∠CDP=∠A+∠APD=45°.所以∠CDP的大小不发生变化.
试题解析:(1)连接OC,
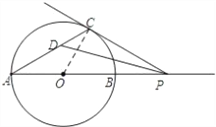
∵PC是⊙O的切线,
∴OC⊥PC
∴∠OCP=90°.
∵∠CPA=30°,
∴∠COP=60°
∵OA=OC,
∴∠A=∠ACO=30°
∵PD平分∠APC,
∴∠APD=15°,
∴∠CDP=∠A+∠APD=45°.
(2)∠CDP的大小不发生变化.
∵PC是⊙O的切线,
∴∠OCP=90°.
∵PD是∠CPA的平分线,
∴∠APC=2∠APD.
∵OA=OC,
∴∠A=∠ACO,
∴∠COP=2∠A,
在Rt△OCP中,∠OCP=90°,
∴∠COP+∠OPC=90°,
∴2(∠A+∠APD)=90°,
∴∠CDP=∠A+∠APD=45°.
即∠CDP的大小不发生变化.

 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案【题目】某校为了备战2018体育中考,因此在八年级抽取了50名女学生进行“一分钟仰卧起坐”测试,测试的情况绘制成表格如下:
个数 | 16 | 22 | 25 | 28 | 29 | 30 | 35 | 37 | 40 | 42 | 45 | 46 |
人数 | 2 | 1 | 7 | 18 | 1 | 9 | 5 | 2 | 1 | 1 | 1 | 2 |
(1)通过计算算得出这50名女学生进行“一分钟仰卧起坐”的平均数是 , 请写出这50名女学生进行“一分钟仰卧起坐”的众数和中位数,它们分别是、 .
(2)学校根据测试数据规定八年级女学生“一分钟仰卧起坐”的合格标准为28次,已知该校五年级有女生250名,试估计该校五年级女生“一分钟仰卧起坐”的合格人数是多少?
【题目】商场某柜台销售每台进价分别为160元、120元的A、B两种型号的电风扇,下表是近两周的销售情况:
销售时段 | 销售数量 | 销售收入 | |
A种型号 | B种型号 | ||
第一周 | 3台 | 4台 | 1200元 |
第二周 | 5台 | 6台 | 1900元 |
(进价、售价均保持不变,利润=销售收入﹣进货成本)
(1)求A、B两种型号的电风扇的销售单价;
(2)若商场准备用不多于7500元的金额再采购这两种型号的电风扇共50台,求A种型号的电风扇最多能采购多少台?
(3)在(2)的条件下,商场销售完这50台电风扇能否实现利润超过1850元的目标?若能,请给出相应的采购方案;若不能,请说明理由.