题目内容
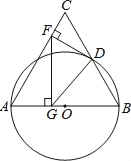
【题目】如图,在△ABC中,∠BAC=90°,AD是高,BE是中线,CF是角平分线,CF交AD于点G,交BE于点H,下面说法不正确的是( )

A.△ABE的面积=△BCE的面积B.∠AFG=∠AGF
C.BH=CHD.∠FAG=2∠ACF
【答案】C
【解析】
根据中线的性质即可判断A,根据直角三角形的锐角互余即可判断B,根据同角的余角相等以及角平分线的性质即可判断D.
根据三角形中线的性质可得:△ABE的面积和△BCE的面积相等,故A正确,
因为∠BAC=90°,所以∠AFG+∠ACF=90°,因为AD是高,所以∠DGC+∠DCG=90°,
因为CF是角平分线,所以∠ACF=∠DCG,所以∠AFG=∠DGC,又因为∠DGC=∠AGF,所以
∠AFG=∠AGF,故B正确,
因为∠FAG+∠ABC=90°,∠ACB+∠ABC=90°,所以∠FAG=∠ACB,又因为CF是角平分线,所以∠ACB=2∠ACF,所以∠FAG=2∠ACF,故D正确,
假设BH=CH,∠ACB=30°,则∠HBC=∠HCB=15°,∠ABC=60°,
所以∠ABE=60°-15°=45°,因为∠BAC=90°,所以AB=AE,因为AE=EC,所以![]() ,这与在直角三角形中30°所对直角边等于斜边的一半相矛盾,所以假设不成立,故④不一定正确,
,这与在直角三角形中30°所对直角边等于斜边的一半相矛盾,所以假设不成立,故④不一定正确,
故选A.

练习册系列答案
 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目