题目内容
(12分)已知,边长为5的正方形ABCO在如图所示的直角坐标系中,点
M(t,0)为x轴上一动点,过A作直线MC的垂线交y轴于点N.
(1)当t=2时,求直线MC的解析式;
(2)设△AMN的面积为S,当S=3时,求t的值;
(3)取点P(1,y),如果存在以M、N、C、P为顶点的四边形是等腰梯形,当t<0时,甲同学说:y与t应同时满足方程t2-yt-5=0和y2-2t2-10y+26=0;乙同学说:y与t应同时满足方程t2-yt-5=0和y2+8t-24=0,你认为谁的说法 正确,并说明理由.再直接写出t>0时满足题意的一个点P的坐标.
正确,并说明理由.再直接写出t>0时满足题意的一个点P的坐标.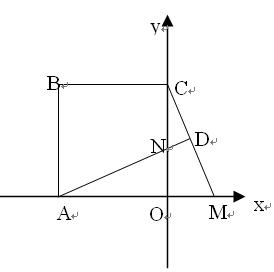
M(t,0)为x轴上一动点,过A作直线MC的垂线交y轴于点N.
(1)当t=2时,求直线MC的解析式;
(2)设△AMN的面积为S,当S=3时,求t的值;
(3)取点P(1,y),如果存在以M、N、C、P为顶点的四边形是等腰梯形,当t<0时,甲同学说:y与t应同时满足方程t2-yt-5=0和y2-2t2-10y+26=0;乙同学说:y与t应同时满足方程t2-yt-5=0和y2+8t-24=0,你认为谁的说法
 正确,并说明理由.再直接写出t>0时满足题意的一个点P的坐标.
正确,并说明理由.再直接写出t>0时满足题意的一个点P的坐标.
(1) 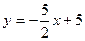 …………(2分)
…………(2分)
( 2)S=
2)S=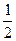 t2+
t2+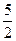 t(t>0)……(1分) t=1……(1分)
t(t>0)……(1分) t=1……(1分)
S=-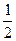 t2-
t2-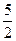 t(-5<t<0)…(1分) t=-2,t=-3 (1分)
t(-5<t<0)…(1分) t=-2,t=-3 (1分)
S=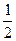 t2+
t2+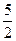 t(t<-5)……(1分) t=-6……(1分)
t(t<-5)……(1分) t=-6……(1分)
(3)都正确,作PH⊥y轴,则△PHN∽△MOC, 得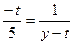 ,
,
所以 t2-yt-5=0, 满足PN∥CM …………(1分)
由Rt△PCH得 1+(y-5)2=2t2,
所以 y2-2t2-10y+26=0,满足PC=MN, 故甲正确……(1分)
直线x=1与x轴交于E,由Rt△PME得,
(5-t)2=y2+(1-t)2
所以 y2+8t-24=0,满足PM=CN, 故乙正确……(1分)
(每个方程1分)
P(1,6)…………(1分)
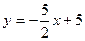 …………(2分)
…………(2分)(
 2)S=
2)S=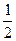 t2+
t2+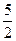 t(t>0)……(1分) t=1……(1分)
t(t>0)……(1分) t=1……(1分) S=-
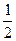 t2-
t2-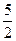 t(-5<t<0)…(1分) t=-2,t=-3 (1分)
t(-5<t<0)…(1分) t=-2,t=-3 (1分)S=
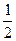 t2+
t2+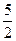 t(t<-5)……(1分) t=-6……(1分)
t(t<-5)……(1分) t=-6……(1分)(3)都正确,作PH⊥y轴,则△PHN∽△MOC, 得
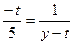 ,
,所以 t2-yt-5=0, 满足PN∥CM …………(1分)
由Rt△PCH得 1+(y-5)2=2t2,
所以 y2-2t2-10y+26=0,满足PC=MN, 故甲正确……(1分)
直线x=1与x轴交于E,由Rt△PME得,
(5-t)2=y2+(1-t)2
所以 y2+8t-24=0,满足PM=CN, 故乙正确……(1分)
(每个方程1分)
P(1,6)…………(1分)
略

练习册系列答案
 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案
相关题目
 中,抛物线
中,抛物线 向左平移1个单位,再向下平移4个单位,得到抛物线
向左平移1个单位,再向下平移4个单位,得到抛物线 .所得抛物线与
.所得抛物线与 轴交于
轴交于 两点(点
两点(点 在点
在点 的左边),与
的左边),与 轴交于点
轴交于点 ,顶点为
,顶点为 .
. 的值;
的值; 上是否存在点
上是否存在点 ,使
,使 与
与 相似.若存在,求出点
相似.若存在,求出点
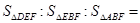 ( ▲ )
( ▲ )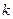 ,若AD︰BC = 2︰3. 请探究:当k为下列三种情况时,四边形ABPE是什么四边形?
,若AD︰BC = 2︰3. 请探究:当k为下列三种情况时,四边形ABPE是什么四边形?


 ,OA的长为半径的圆交边CD于点M,连接OM,过点M作圆O的切线交边BC于点N.
,OA的长为半径的圆交边CD于点M,连接OM,过点M作圆O的切线交边BC于点N.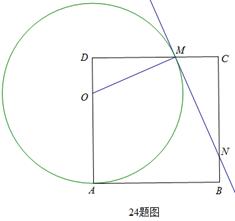
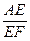 的值.
的值.
