题目内容
【题目】如图，正方形
的对角线
，
相交于点
．
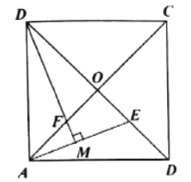
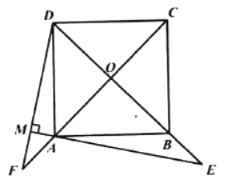
（1） （2）
（1）若点
是上一点，连接
，过点
作
，垂足为
，
与相交于点
．求证：
；
（2）若点在
的延长线上，于点，交
的延长线于点，其他条件不变结论“”还成立吗？如果成立，请给出证明；如果不成立，请说明理由．
【答案】（1）证明见解析；（2）“OE = OF”仍然成立；理由见解析．
【解析】
（1）由四边形ABCD为平行四边形，得到对角线垂直且互相平分，再由DM与AE垂直，得到一组对角相等，进而得到
≌
，利用全等三角形对应边相等即可得证；
（2）其他条件不变．结论“OE=OF”还成立，理由为：同（1）得到全等三角形，即可得证．
（1）证明：∵正方形ABCD的对角线AC，BD相交于点O，
∴
，
．
∴
∵
，
，
∴
．
∴≌．
∴
．
（2）结论：“OE = OF”仍然成立
证明：∵正方形ABCD的对角线AC，BD相交于点O，
∴，．
∴．
∵，
，
∴
．
∴≌．
∴．
练习册系列答案
新非凡教辅冲刺100分系列答案
相关题目
【题目】“2018东台西溪半程马拉松”的赛事共有两项：A、“半程马拉松”、 B、“欢乐跑”。小明参加了该项赛事的志愿者服务工作， 组委会随机将志愿者分配到两个项目组．
（1）小明被分配到“半程马拉松”项目组的概率为________．
（2）为估算本次赛事参加“半程马拉松”的人数，小明对部分参赛选手作如下调查：
调查总人数 | 20 | 50 | 100 | 200 | 500 |
参加“半程马拉松”人数 | 15 | 33 | 72 | 139 | 356 |
参加“半程马拉松”频率 | 0.750 | 0.660 | 0.720 | 0.695 | 0.712 |
①请估算本次赛事参加“半程马拉松”人数的概率为_______．（精确到0.1）
②若本次参赛选手大约有3000人，请你估计参加“半程马拉松”的人数是多少？
