Question

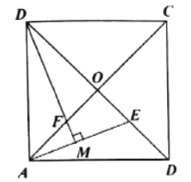
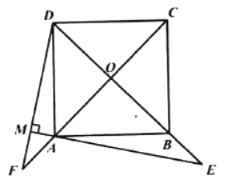
【题目】如图，在菱形ABCD的对角线相交于点O，延长AB至点E，使BE＝AB，连接CE，∠E＝50°．

（1）求证：BD＝EC；

（2）求∠BAO的大小．

Answer 1

【答案】（1）见解析；（2）40°

【解析】

（1）先证明四边形BECD是平行四边形，再利用平行四边形的性质即可证明；

（2）先说明BD//CE，再利用平行线的性质得到∠ABO=∠E=50°；再由菱形的性质可得AC⊥BD，最后根据直角三角形的性质即可解答．

（1）证明：∵四边形ABCD是菱形，

∴AB＝CD，AB∥CD，

又∵BE＝AB，

∴BE＝CD，BE∥CD，

∴四边形BECD是平行四边形，

∴BD＝EC；

（2）解：∵四边形BECD是平行四边形，

∴BD∥CE，∴∠ABO＝∠E＝50°，

又∵四边形ABCD是菱形，

∴AC⊥BD，

∴∠BAO＝90°﹣∠ABO＝40°