题目内容
【题目】已知一次函数![]() 和
和![]() .
.
(1)在同一直角坐标系内,画出这两个函数的大致图象;

(2)直接写出:①函数![]() 与坐标轴围成的图形的面积为_______;
与坐标轴围成的图形的面积为_______;
②函数![]() 与坐标轴围成的图形的面积为________;
与坐标轴围成的图形的面积为________;
③这两个函数图象与![]() 轴围成的图形的面积为_________.
轴围成的图形的面积为_________.
(3)若反比例函数![]() 经过这两个函数图象的交点,则k的值为______.
经过这两个函数图象的交点,则k的值为______.
【答案】(1)画出这两个函数的大致图象见解析;(2)① ![]() ;②
;② ![]() ;③
;③ ![]() ;(3)3.
;(3)3.
【解析】
(1)把x=0,x=-1分别代入![]() 得出y值,描出两点,作出过两点的直线即可得
得出y值,描出两点,作出过两点的直线即可得![]() 的图象;把x=-1,x=-2分别代入
的图象;把x=-1,x=-2分别代入![]() 得出y值,描出两点,作出过两点的直线即可得
得出y值,描出两点,作出过两点的直线即可得![]() 的图象;
的图象;
(2)①分别令x=0,y=0,可分别求出x、y的值,根据直线与坐标轴围成的图形的面积=![]() |x||y|即可得答案;
|x||y|即可得答案;
②分别令x=0,y=0,可分别求出x、y的值,根据直线与坐标轴围成的图形的面积=![]() |x||y|即可得答案;
|x||y|即可得答案;
③由①②可知两直线与x轴的交点坐标,联立两直线解析式,解方程组可求出两直线的交点坐标,即可求出两个函数图象与![]() 轴围成的图形的面积;
轴围成的图形的面积;
(3)把两图象的交点坐标代入反比例函数解析式可求出k值,即可得答案.
(1)当x=0时,![]() =1,当x=-1时,
=1,当x=-1时,![]() =-3,
=-3,
当x=-1时,![]() =-3,当x=-2时,
=-3,当x=-2时,![]() =-1,
=-1,
∴两个函数的大致图象如图所示:
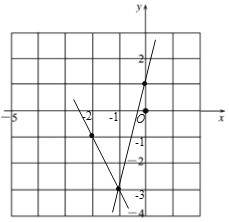
(2)①当x=0时,y=4x+1=1,
当y=0时,4x+1=0,
解得:x=![]() ,
,
∴函数![]() 与坐标轴围成的图形的面积为
与坐标轴围成的图形的面积为![]() ×|
×|![]() |×|1|=
|×|1|=![]() ,
,
故答案为:![]()
②当x=0时,y=-2x-5=-5,
当y=0时,-2x-5=0,
解得:x=![]() ,
,
∴函数y=-2x-5与坐标轴围成的图形的面积为![]() ×|
×|![]() |×|-5|=
|×|-5|=![]() ,
,
故答案为:![]()
③联立两直线解析式得:![]() ,
,
解得:![]() ,
,
∴两直线的交点坐标为(-1,-3),
由①②可知两直线与x轴当交点坐标为(![]() ,0)和(
,0)和(![]() ,0),
,0),
∴两个函数图象与![]() 轴围成的图形的面积为
轴围成的图形的面积为![]() ×|
×|![]() -(
-(![]() )|×|-3|=
)|×|-3|=![]() ,
,
故答案为:![]()
(3)∵两直线的交点坐标为(-1,-3),
∴k=(-1)×(-3)=3,
故答案为:3

 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案