Question

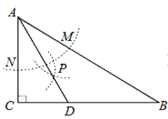
【题目】问题情境：在等腰直角三角形ABC中，， 直线过点且，过点为一锐角顶点作，且点在直线上（不与点重合），如图1， 与交于点，试判断与的数量关系，并说明理由．探究展示：小星同学展示出如下正确的解法：

解：，证明如下：

过点作，交于点

则为等腰直角三角形

（依据）

在与中

（依据）

（1）反思交流：上述证明过程中的“依据”和“依据”分别是指：

依据：

依据：

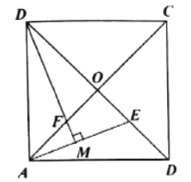
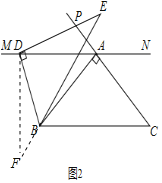
拓展延伸：（2）在图2中，与延长线交于点，试判断与的数量关系，并写出证明过程

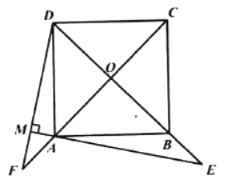
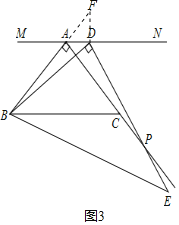
（3）在图3中，与延长线交于点，试判断与的数量关系，并写出证明过程．

Answer 1

【答案】（1）依据：同角的余角相等，依据：全等三角形的对应边相等；（2），见解析；（3）BD=DP，见解析

【解析】

（1）根据余角的概念、全等三角形的性质解答；

（2）作DF⊥MN交AB的延长线于F，证明△BDF≌△PDA，根据全等三角形的性质证明结论；

（3）作DF⊥MN交BA的延长线于F，证明△BDF≌△PDA，根据全等三角形的性质证明结论．

依据:同角的余角相等

依据:全等三角形的对应边相等；

故答案为：同角的余角相等；全等三角形的对应边相等；

成立.

如图2,过点作,交的延长线于点

则为等腰直角三角形，

∴，

∴∠FDB=∠ADP，

在与中，

∴∠FDB=∠ADP，

BD=DP.

如答图3,过点作，交的延长线于点

则为等腰直角三角形，

在与中，