题目内容
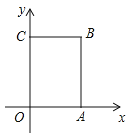
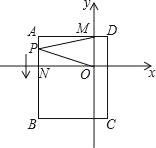
【题目】如图,平面直角坐标系中,ABCD为长方形,其中点A、C坐标分别为(﹣8,4)、(2,﹣8),且AD∥x轴,交y轴于M点,AB交x轴于N.
(1)求B、D两点坐标和长方形ABCD的面积;
(2)一动点P从A出发(不与A点重合),以![]() 个单位/秒的速度沿AB向B点运动,在P点运动过程中,连接MP、OP,请直接写出∠AMP、∠MPO、∠PON之间的数量关系;
个单位/秒的速度沿AB向B点运动,在P点运动过程中,连接MP、OP,请直接写出∠AMP、∠MPO、∠PON之间的数量关系;
(3)是否存在某一时刻t,使三角形AMP的面积等于长方形面积的![]() ?若存在,求t的值并求此时点P的坐标;若不存在请说明理由.
?若存在,求t的值并求此时点P的坐标;若不存在请说明理由.
【答案】(1)B(﹣8,﹣8),D(2,4),120;(2)∠MPO=∠AMP+∠PON;∠MPO=∠AMP-∠PON;(3)存在,P点坐标为(﹣8,﹣6).
【解析】
(1)利用点A、C的坐标和长方形的性质易得B(﹣8,﹣8),D(2,4),然后根据长方形的面积公式即可计算长方形ABCD的面积;
(2)分点P在线段AN上和点P在线段NB上两种情况进行讨论即可得;
(3)由于AM=8,AP=![]() t,根据三角形面积公式可得S△AMP =t,再利用三角形AMP的面积等于长方形面积的
t,根据三角形面积公式可得S△AMP =t,再利用三角形AMP的面积等于长方形面积的![]() ,即可计算出t=20,从而可得AP=10,再根据点的坐标的表示方法即可写出点P的坐标.
,即可计算出t=20,从而可得AP=10,再根据点的坐标的表示方法即可写出点P的坐标.
(1)∵点A、C坐标分别为(﹣8,4)、(2,﹣8),
∴B(﹣8,﹣8),D(2,4),
长方形ABCD的面积=(2+8)×(4+8)=120;
(2)当点P在线段AN上时,作PQ∥AM,如图,
∵AM∥ON,∴AM∥PQ∥ON,∴∠QPM=∠AMP,∠QPO=∠PON,
∴∠QPM+∠QPO=∠AMP+∠PON,即∠MPO=∠AMP+∠PON;
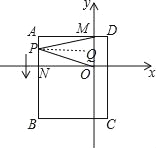
当点P在线段NB上时,作PQ∥AM,如图,
∵AM∥ON,∴AM∥PQ∥ON,∴∠QPM=∠AMP,∠QPO=∠PON,
∴∠QPM-∠QPO=∠AMP-∠PON,即∠MPO=∠AMP-∠PON;

(3)存在,
∵AM=8,AP=![]() t,∴S△AMP=
t,∴S△AMP=![]() ×8×
×8×![]() t=2t,
t=2t,
∵三角形AMP的面积等于长方形面积的![]() ,
,
∴2t=120×![]() =40,∴t=20,AP=
=40,∴t=20,AP=![]() ×20=10,
×20=10,
∵AN=4,
∴PN=6
∴P点坐标为(﹣8,﹣6).

 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案