题目内容
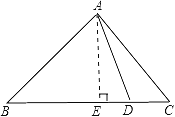
【题目】如图,在△ABC中,∠BAC=90°,AB=AC,D是BC上的点.求证:BD2+CD2=2AD2.
【答案】证明过程见解析
【解析】
试题分析:作AE⊥BC于E,由于∠BAC=90°,AB=AC,所以BE=CE,要证明BD2+CD2=2AD2,只需找出BD、CD、AD三者之间的关系即可,由勾股定理可得出AD2=AE2+ED2,AE2=AB2﹣BE2=AC2﹣CE2,ED=BD﹣BE=CE﹣CD,代入求出三者之间的关系即可得证.
试题解析:作AE⊥BC于E,如上图所示: 由题意得![]() :ED=BD﹣BE=CE﹣CD,
:ED=BD﹣BE=CE﹣CD,
∵在△ABC中,∠BAC=90°,AB=AC, ∴BE=CE=BC, 由勾股定理可得:
AB2+AC2=BC2, AE2=AB2﹣BE2=AC2﹣CE2, AD2=AE2+ED2,
∴2AD2=2AE2+2ED2=AB2﹣BE2+(BD﹣BE)2+AC2﹣CE2+(CE﹣CD)2
=AB2+AC2+BD2+CD2﹣2BD×BE﹣2CD×CE =AB2+AC2+BD2+CD2﹣2×![]() BC×BC
BC×BC
=BD2+CD2, 即:BD2+CD2=2AD2.

练习册系列答案
相关题目