题目内容
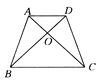
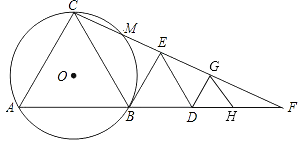
【题目】已知，如图，△ABC是等边三角形，四边形BDEF是菱形，其中线段DF的长与DB相等，将菱形BDEF绕点B按顺时针方向旋转，甲、乙两位同学发现在此旋转过程中，有如下结论．
甲：线段AF与线段CD的长度总相等；
乙：直线AF和直线CD所夹的锐角的度数不变；
那么，你认为（ ）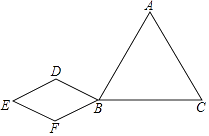
A.甲、乙都对
B.乙对甲不对
C.甲对乙不对
D.甲、乙都不对
【答案】A
【解析】解：连接DF，AF，CD，如图，
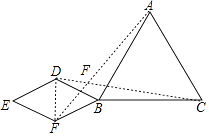
∵四边形BDEF为菱形，
∴BD=BF，
而DF=BD，
∴△BDF为等边三角形，
∴∠DBF=60°，
∵△ABC为等边三角形，
∴BA=BC，∠ABC=60°，
∴∠ABF=∠CBD，
∴△ABF绕点B顺时针旋转60°可得到△CBD，
∴AF=CD，∠FBA=∠DBC，
∴∠AFC=∠ABC=60°，
即直线AF和直线CD所夹的锐角的度数为60°．
所以答案是：A．
【考点精析】根据题目的已知条件，利用等边三角形的性质和菱形的性质的相关知识可以得到问题的答案，需要掌握等边三角形的三个角都相等并且每个角都是60°；菱形的四条边都相等；菱形的对角线互相垂直，并且每一条对角线平分一组对角；菱形被两条对角线分成四个全等的直角三角形；菱形的面积等于两条对角线长的积的一半．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
